
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{4}{3}$ |
分析 由已知得X~B(3,$\frac{1}{3}$),由此能求出E(X),D(X),即可得出结论.
解答 解:袋中有15个除了颜色外完全相同的球,其中有10个白球,5个红,从中任取1球,记住颜色后再放回,连续摸取3次,
则每次取到红球的概率都是P=$\frac{5}{15}$=$\frac{1}{3}$,
设X为取得红球的次数,则X~B(3,$\frac{1}{3}$),
∴E(X)=3×$\frac{1}{3}$=1,D(X)=3×$\frac{1}{3}$×(1-$\frac{1}{3}$)=$\frac{2}{3}$,
∴E(X)+D(X)=$\frac{5}{3}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意二项分布的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
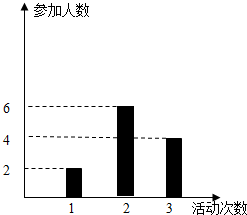 某城市号召中学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该城市某学校学生会共有12名学生,他们参加活动的次数统计如图所示.
某城市号召中学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该城市某学校学生会共有12名学生,他们参加活动的次数统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
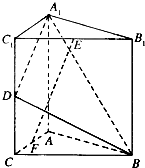 如图,在直三棱柱ABC-A1B1C1中,C1C=CB=CA=2,AC⊥CB,D,E分别为棱C1C,B1C1的中点.
如图,在直三棱柱ABC-A1B1C1中,C1C=CB=CA=2,AC⊥CB,D,E分别为棱C1C,B1C1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com