考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)以C点为原点,CA所在直线为x轴,CB所在直线为y轴,以CC1所在直线为z轴,建立空间直角坐标系,利用向量法能证明CD⊥平面A1DE.
(2)分别求出平面A1DC的法向量和平面A1CA的法向量,利用向量法能求出二面角D-A1C-A的余弦值.
解答:
解:(1)以C点为原点,CA所在直线为x轴,CB所在直线为y轴,
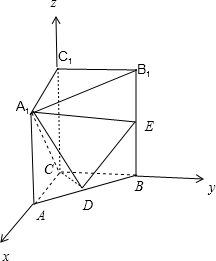
以CC
1所在直线为z轴,建立空间直角坐标系,
则C(0,0,0),A(2,0,0),B(0,2,0),
A
1(2,0,2),B
1(0,2,2),D(1,1,0),E(0,2,1),
∴
=(1,1,0),
=(-1,1,-2),
=(-1,1,1).
∵
•=0,
•=0.
∴线段CD⊥线段A
1D,线段CD⊥线段DE,
∴CD⊥平面A
1DE.
(2)
=(2,0,2),
=(1,1,0).
设平面A
1DC的法向量
=(x,y,z).
则
,取z=1,得
=(-1,1,1).
又∵CB⊥平面A
1CA,
=(0,2,0)就是平面A
1CA的一个法向量.
设二面角D-A
1C-A的平面角为θ,
cosθ=|cos<
,>|=|
|=
,
∴二面角D-A
1C-A的余弦值为
.
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要注意向量法的合理运用.

 如图所示,已知直三棱柱ABC-A1B1C1中,AC=CB=AA1=2,∠ACB=90°,E为BB1的中点,D∈AB,∠A1DE=90°.
如图所示,已知直三棱柱ABC-A1B1C1中,AC=CB=AA1=2,∠ACB=90°,E为BB1的中点,D∈AB,∠A1DE=90°.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案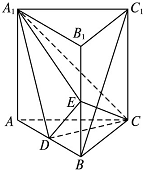 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.