练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．下面结论正确的是（　　）
    ①一个数列的前三项是1，2，3，那么这个数列的通项公式是an=n（n∈N*）．
    ②由平面三角形的性质推测空间四面体的性质，这是一种合情推理．
    ③在类比时，平面中的三角形与空间中的平行六面体作为类比对象较为合适．
    ④“所有3的倍数都是9的倍数，某数m是3的倍数，则m一定是9的倍数”，这是三段论推理，但其结论是错误的．
    A．①②B．②③C．③④D．②④

    分析 举例说明①错误；由合情推理的概念说明②正确；在类比时，平面中的三角形与空间中的四面体作为类比对象较为合适，可知③错误；由大前提“所有3的倍数都是9的倍数”错误可判断④．

    解答 解：①一个数列的前三项是1，2，3，那么这个数列的通项公式是an=n（n∈N*）错误，如数列1，2，3，5．
    ②由平面三角形的性质推测空间四面体的性质，这是一种合情推理，且是类比推理，正确．
    ③在类比时，平面中的三角形与空间中的四面体作为类比对象较为合适，故③错误．
    ④“所有3的倍数都是9的倍数，某数m是3的倍数，则m一定是9的倍数”，这是三段论推理，但其结论是错误的，原因是大前提“所有3的倍数都是9的倍数”错误，故④正确．
    ∴正确的命题是②④．
    故选：D．

    点评 本题考查命题的真假判断与应用，考查合情推理与演绎推理，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．江湖传说，蜀中唐门配制的天下第一奇毒“含笑半步癫”是由3种藏红花，2种南海蛇毒和1种西域毒草顺次添加炼制而成，其中藏红花的添加顺序不能相邻，同时南海蛇毒的添加顺序也不能相邻，现要研究所有不同添加顺序对药效的影响，则总共要进行48次试验．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．复数z1、z2满足|z1|=|z2|=1，z1-z2=$\frac{2-4i}{2+i}$，则z1•z2=（　　）
    A．1B．-1C．iD．-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知函数f（x）=$\frac{sinx}{2+cosx}$，如果当x＞0时，若函数f（x）的图象恒在直线y=kx的下方，则k的取值范围是（　　）
    A．[$\frac{1}{3}$，$\frac{\sqrt{3}}{3}$]B．[$\frac{1}{3}$，+∞）C．[$\frac{\sqrt{3}}{3}$，+∞）D．[-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．在△ABC中，a，b，c分别是角A，B，C的对边，若a=1，b=$\sqrt{3}$，B=60°，则△ABC的面积为（　　）
    A．$\frac{1}{2}$B．$\frac{\sqrt{3}}{2}$C．1D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．阅读如图所示的程序框图，运行相应的程序，则输出i的值为（　　）
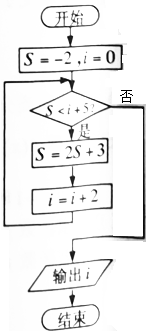
    A．4B．6C．8D．10

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．若向量$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（2，1），$\overrightarrow{c}$=（-4，-2），则下列说法中正确的个数是（　　）
    ①$\overrightarrow{a}$⊥$\overrightarrow{b}$；②向量$\overrightarrow{a}$与向量$\overrightarrow{c}$的夹角为90°；③对同一平面内的任意向量$\overrightarrow{d}$，都存在一对实数k1，k2，使得$\overrightarrow{d}$=k1$\overrightarrow{b}$+k2$\overrightarrow{c}$．
    A．3B．2C．1D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知命题p：△ABC中，若A＞B，则cosA＞cosB，则下列命题为真命题的是（　　）
    A．p的逆命题B．p的否命题C．p的逆否命题D．p的否定

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若存在正实数m，使得关于x的方程x+a（2x+2m-4ex）[1n（x+m）-lnx]=0有两个不同的根，其中e为自然对数的底数，则实数a的取值范围是（　　）
    A．（-∞，0）B．（0，$\frac{1}{2e}$）C．（-∞，0）∪（$\frac{1}{2e}$，+∞）D．（$\frac{1}{2e}$，+∞）

    查看答案和解析>>

    同步练习册答案