
在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2b-c)cos A-acos C=0.
(1)求角A的大小;
(2)若a=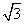 ,S△ABC=
,S△ABC=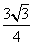 ,试判断△ABC的形状,并说明理由.
,试判断△ABC的形状,并说明理由.
解:(1)法一:由(2b-c)cos A-acos C=0及正弦定理,得
(2sin B-sin C)cos A-sin Acos C=0,
∴2sin Bcos A-sin(A+C)=0,
sin B(2cos A-1)=0.
∵0<B<π,∴sin B≠0,∴cos A=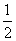 .
.
∵0<A<π,∴A= .
.
法二:由(2b-c)cos A-acos C=0,
及余弦定理,得(2b-c)· =0,整理,得b2+c2-a2=bc,
=0,整理,得b2+c2-a2=bc,
∴cos A= =
=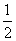 ,
,
∵0<A<π,∴A= .
.
(2)△ABC为等边三角形.
∵S△ABC=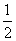 bcsin A=
bcsin A=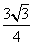 ,
,
即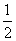 bcsin
bcsin =
=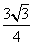 ,
,
∴bc=3,①
∵a2=b2+c2-2bccos A,a=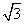 ,A=
,A= ,
,
∴b2+c2=6,②
由①②得b=c=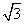 ,
,
∴△ABC为等边三角形.


科目:高中数学 来源: 题型:
如图,在平行四边形ABCD中,O是对角线AC,BD的交点,N是线段OD的中点,AN的延长线与CD交于点E,则下列说法错误的是( )
 A.
A.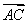 =
=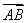 +
+
B. =
= -
-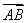
C.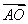 =
=
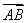 +
+

D. =
=
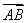 +
+
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=3cos(ωx+φ)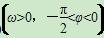 的最小正周期为π,且其图像经过点
的最小正周期为π,且其图像经过点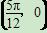 .
.
(1)求函数f(x)的解析式;
(2)若函数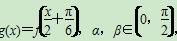 ,且g(α)=1,g(β)=
,且g(α)=1,g(β)=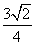 ,求g(α-β)的值.
,求g(α-β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
在不等边三角形ABC中,角A、B、C所对的边分别为a、b、c,其中a为最大边,如果sin2(B+C)<sin2B+sin2C,则角A的取值范围为( )
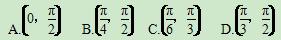
查看答案和解析>>
科目:高中数学 来源: 题型:
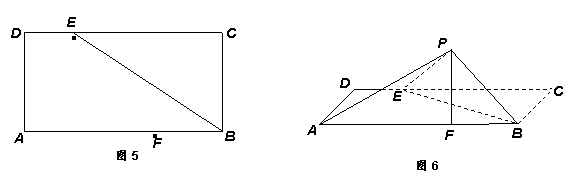
如图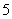 ,矩形
,矩形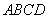 中,
中,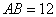 ,
,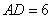 ,
,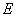 、
、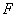 分别为
分别为 、
、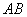 边上的点,且
边上的点,且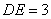 ,
,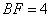 ,将
,将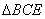 沿
沿 折起至
折起至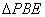 位置(如图
位置(如图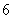 所示),连结
所示),连结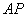 、
、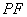 ,其中
,其中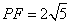 .
.
(Ⅰ) 求证: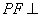 平面
平面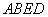 ;
;
(Ⅱ) 在线段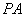 上是否存在点
上是否存在点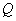 使得
使得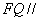 平面
平面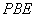 ?若存在,求出点
?若存在,求出点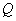 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(Ⅲ) 求点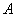 到平面
到平面 的距离.
的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com