
分析 (Ⅰ)求出线段AB的垂直平分线的方程,结合圆C的圆心C在直线x-y+2=0上,又在y轴上,求出圆心坐标与半径,即可求圆C的方程;
(Ⅱ)由题意,分类讨论,设方程,利用直线被圆C截得的弦长为$\sqrt{2}$,可得圆心到直线的距离为$\frac{\sqrt{2}}{2}$,即可求出直线的方程.
解答 解:(Ⅰ)由已知,得线段AB的中点坐标为($\frac{1}{2}$,$\frac{5}{2}$),
直线AB的斜率kAB=$\frac{3-2}{0-1}$=-1,
所以线段AB的垂直平分线的方程为y-$\frac{5}{2}$=x-$\frac{1}{2}$,即x-y+2=0.
由题意,圆C的圆心C在直线x-y+2=0上,又在y轴上,所以C(0,2),
半径r=|BC|=1,所以圆C的方程为x2+(y-2)2=1. ….(6分)
(Ⅱ)由题意,直线不过原点,设方程为x+y-a=0,
∵直线被圆C截得的弦长为$\sqrt{2}$,
∴圆心到直线的距离为$\frac{\sqrt{2}}{2}$,
∴$\frac{|a-2|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴a=1或3,
∴所求直线方程为x+y-1=0或x+y-3=0,
直线过原点,设直线l的方程为y=kx.∴$\frac{|2|}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{2}}{2}$,
∴k=$±\sqrt{7}$x,∴所求直线方程为y=$±\sqrt{7}$x.
综上所述所求直线为x+y-1=0或x+y-3=0或y=$±\sqrt{7}$x.
点评 本题考查了圆的方程、直线的基本量与基本形式、点到直线的距离公式和直线与圆的位置关系等知识,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届湖南永州市高三高考一模考试数学(文)试卷(解析版) 题型:选择题
某学校高一、高二、高三年级的学生人数之比为4:3:3,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则从高二年级抽取的学生人数为( )
A.15 B.20 C.25 D.30
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,且AC=BC=5,SB=$5\sqrt{5}$.(如图所示)
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,且AC=BC=5,SB=$5\sqrt{5}$.(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
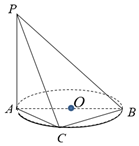 如图,AB是⊙O的直径,P是⊙O所在平面外一点,PA垂直于⊙O所在平面,且PA=AB=10,设点C为⊙O上异于A、B的任意一点.
如图,AB是⊙O的直径,P是⊙O所在平面外一点,PA垂直于⊙O所在平面,且PA=AB=10,设点C为⊙O上异于A、B的任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{100}$,100) | B. | (100,+∞) | C. | ($\frac{1}{100}$,+∞) | D. | (0,$\frac{1}{100}$)∪(100,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,m?α,则l∥m | B. | 若l∥m,m?α,则l∥α | C. | 若l⊥m,m?α,则l⊥α | D. | 若l⊥α,m?α,则l⊥m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com