
分析 (1)利用导数判断出f(x)的单调性,求出f(x)的最大值即可得出结论;
(2)利用中值定理得出f′(x)<4在(1,+∞)上恒成立,使用分离参数法求出a的范围即可;
(3)分离参数得a=$\frac{2lnx-{x}^{2}}{2x-{x}^{2}}$,求出右侧函数的值域即为a的取值范围.
解答 解:(1)证明:a=1时,f(x)=lnx-x,f′(x)=$\frac{1}{x}-1$.
∴当0<x<1时,f′(x)>0,当x>1时,f′(x)<0,当x=1时,f′(x)=0,
∴f(x)在(0,1)上单调递增,在[1,+∞)上单调递减,
当x=1时,f(x)取得最大值f(1)=-1.
∴f(x)≤-1.
(2)∵函数f(x)在区间(1,+∞)上任意两点的连线段的斜率都小于4,
∴f′(x)=$\frac{1}{x}-a$<4在(1,+∞)上恒成立,即a>$\frac{1}{x}-4$在(1,+∞)上恒成立,
令g(x)=$\frac{1}{x}-4$,则g(x)在(1,+∞)上单调递减,g(1)=-3.
∴a≥-3.
即a的最小值为-3.
(3)由f(x)=-$\frac{a-1}{2}{x}^{2}$得lnx-ax+$\frac{a-1}{2}{x}^{2}$=0,∴a=$\frac{2lnx-{x}^{2}}{2x-{x}^{2}}$.
令h(x)=$\frac{2lnx-{x}^{2}}{2x-{x}^{2}}$,得h′(x)=$\frac{2(x-1)(2lnx-x-2)}{(2x-{x}^{2})^{2}}$.
令m(x)=2lnx-x-2,则m′(x)=$\frac{2}{x}-1$,
∴m(x)在(0,1)单调递增,在(1,+∞)上单调递减,
∴mmax(x)=m(1)=-3<0.∴m(x)=2ln-x-2<0.
令h′(x)=$\frac{2(x-1)(2lnx-x-2)}{(2x-{x}^{2})^{2}}$=0得x=1,
∴当0<x<1时,h′(x)>0,当x>1且x≠2时,h′(x)<0.
∴h(x)在(0,1]上单调递增,在(1,2)上单调递减,在(2,+∞)上单调递减.
∵h(1)=-1,当x→2+时,h(x)→+∞,当x→2-时,h(x)→-∞,当x→+∞时,h(x)→1.
∴h(x)的值域为(-∞,-1]∪(1,+∞).
∴实数a的取值范围是(-∞,-1]∪(1,+∞).
点评 本题考查了导数与函数的单调性,函数最值的关系,导数的几何意义,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 1或-$\frac{1}{2}$ | D. | -1或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
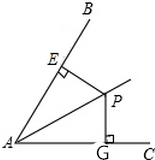 如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PG,则下列哪一个能作为△PEA≌△PGA的理由( )
如图,点P是∠BAC内一点,且P到AB、AC的距离PE=PG,则下列哪一个能作为△PEA≌△PGA的理由( )| A. | HL | B. | AAS | C. | SSS | D. | ASA |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 28 | C. | 26 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com