练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知椭圆C：$\frac{x^2}{16}+\frac{y^2}{12}=1$，点M与C的焦点不重合，若M关于C的两焦点的对称点分别为P，Q，线段MN的中点在C上，则|PN|+|QN|=16．

    分析 先作出图形，由椭圆方程，得a的值，设F1，F2分别是椭圆C的左、右焦点，K为线段MN的中点，易得KF1，KF2分别是△NBM和△NAM的中位线，可得|NB|与|KF1|，及|NA|与|KF2|的数量关系，再利用椭圆的定义，即可达到目的．

    解答 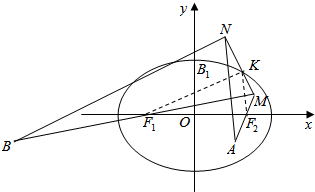解：设椭圆C的长轴长为2a，则由$\frac{x^2}{16}+\frac{y^2}{12}=1$，得a=4，
    又设F1，F2分别是椭圆C的左、右焦点，K为线段MN的中点，
    如右图所示，由已知条件，易得F1，F2分别是线段MB，MA的中点，
    则在△NBM和△NAM中，有|NB|=2|KF1|，|NA|=2|KF2|，
    又由椭圆定义，得|KF1|+|KF2|=2a=8，
    故|AN|+|BN|=2（|KF1|+|KF2|）=16．
    故答案为：16．

    点评 本题主要考查了椭圆定义的运用，三角形中位线的性质等．本题涉及的动点较多，解题的突破口是作出图形，根据图形的几何特征，寻找两个三角形的中位线，关键是利用椭圆的定义，抓住变化中确定的数量关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．函数f（x）=$\sqrt{4-|x|}$+lg$\frac{{{x^2}-5x+6}}{x-3}$的定义域为（　　）
    A．（2，3）B．（2，4]C．（2，3）∪（3，4]D．（-1，3）∪（3，6]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

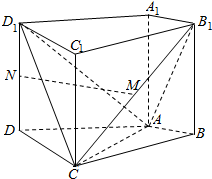    12．如图，在四棱柱ABCD-A1B1C1D1中，侧棱AA1⊥底面ABCD，AB⊥AC，AB=1，AC=AA1=2，AD=CD=$\sqrt{5}$，且点M和N分别为B1C和D1D的中点．
    （Ⅰ）求证：MN∥平面ABCD
    （Ⅱ）求二面角D1-AC-B1的正弦值；
    （Ⅲ）设E为棱A1B1上的点，若直线NE和平面ABCD所成角的正弦值为$\frac{1}{3}$，求线段A1E的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知数列{an}满足a1=$\frac{1}{2}$且an+1=an-an2（n∈N*）
    （1）证明：1＜$\frac{a_n}{{{a_{n+1}}}}$≤2（n∈N*）；
    （2）设数列{an2}的前n项和为Sn，证明$\frac{1}{2（n+2）}≤\frac{S_n}{n}≤\frac{1}{2（n+1）}$（n∈N*）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=3+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$（t为参数），以原点为极点，x轴正半轴为极轴建立极坐标系，⊙C的极坐标方程为ρ=2$\sqrt{3}$sinθ．
    （Ⅰ）写出⊙C的直角坐标方程；
    （Ⅱ）P为直线l上一动点，当P到圆心C的距离最小时，求P的直角坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．在平面直角坐标系xOy中，圆O：x2+y2=1，P为直线l：x=t（1＜t＜2）上一点．
    （1）已知t=$\frac{4}{3}$．
    ①若点P在第一象限，且OP=$\frac{5}{3}$，求过点P的圆O的切线方程；
    ②若存在过点P的直线交圆O于点A，B，且B恰为线段AP的中点，求点P纵坐标的取值范围；
    （2）设直线l与x轴交于点M，线段OM的中点为Q，R为圆O上一点，且RM=1，直线RM与圆O交于另一点N，求线段NQ长的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．设函数f（x）=ln（x+1）+a（x2-x），其中a∈R，
    （Ⅰ）讨论函数f（x）极值点的个数，并说明理由；
    （Ⅱ）若?x＞0，f（x）≥0成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=ln$\frac{1+x}{1-x}$，
    （Ⅰ）求曲线y=f（x）在点（0，f（0））处的切线方程；
    （Ⅱ）求证，当x∈（0，1）时，f（x）＞$2（x+\frac{{x}^{3}}{3}）$；
    （Ⅲ）设实数k使得f（x）$＞k（x+\frac{{x}^{3}}{3}）$对x∈（0，1）恒成立，求k的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知${\overrightarrow e_1}，{\overrightarrow e_2}$是空间单位向量，${\overrightarrow e_1}•{\overrightarrow e_2}=\frac{1}{2}$，若空间向量$\overrightarrow b$满足$\overrightarrow b•{\overrightarrow e_1}=2，\overrightarrow b•{\overrightarrow e_2}=\frac{5}{2}$，且对于任意x，y∈R，$|{\overrightarrow b-（x\overrightarrow{e_1}+y\overrightarrow{e_2}）}|≥|{\overrightarrow b-（{x_0}\overrightarrow{e_1}+{y_0}\overrightarrow{e_2}）}|$=1（x0，y0∈R），则x0=1，y0=2，$|{\overrightarrow b}$|=2$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案