
【题目】如图,在四棱锥![]() 中,
中,![]() ,∠ABD=∠ADB.
,∠ABD=∠ADB.
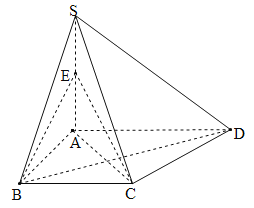
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,求平面
的中点,求平面![]() 切割三棱锥
切割三棱锥![]() 得到的上下两个几何体的体积之比.
得到的上下两个几何体的体积之比.
科目:高中数学 来源: 题型:
【题目】改革开放![]() 年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各
年,我国经济取得飞速发展,城市汽车保有量在不断增加,人们的交通安全意识也需要不断加强.为了解某城市不同性别驾驶员的交通安全意识,某小组利用假期进行一次全市驾驶员交通安全意识调查.随机抽取男女驾驶员各![]() 人,进行问卷测评,所得分数的频率分布直方图如图所示在
人,进行问卷测评,所得分数的频率分布直方图如图所示在![]() 分以上为交通安全意识强.
分以上为交通安全意识强.

![]() 求
求![]() 的值,并估计该城市驾驶员交通安全意识强的概率;
的值,并估计该城市驾驶员交通安全意识强的概率;
![]() 已知交通安全意识强的样本中男女比例为
已知交通安全意识强的样本中男女比例为![]() ,完成下列
,完成下列![]() 列联表,并判断有多大把握认为交通安全意识与性别有关;
列联表,并判断有多大把握认为交通安全意识与性别有关;
安全意识强 | 安全意识不强 | 合计 | |
男性 | |||
女性 | |||
合计 |
![]() 用分层抽样的方式从得分在
用分层抽样的方式从得分在![]() 分以下的样本中抽取
分以下的样本中抽取![]() 人,再从
人,再从![]() 人中随机选取
人中随机选取![]() 人对未来一年内的交通违章情况进行跟踪调查,求至少有
人对未来一年内的交通违章情况进行跟踪调查,求至少有![]() 人得分低于
人得分低于![]() 分的概率.
分的概率.
附: 其中
其中![]()
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .以极点为原点,极轴为
.以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,求曲线
,求曲线![]() 的直角坐标方程以及直线
的直角坐标方程以及直线![]() 的极坐标方程;
的极坐标方程;
(2)设点![]() ,曲线
,曲线![]() 与直线
与直线![]() 交于两点,求
交于两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】单位正方体ABCD-![]() ,黑、白两蚂蚁从点A出发沿棱向前爬行,每走完一条棱称为“走完一段”.白蚂蚁爬地的路线是AA1→A1D1→‥,黑蚂蚁爬行的路线是AB→BB1→‥,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i
,黑、白两蚂蚁从点A出发沿棱向前爬行,每走完一条棱称为“走完一段”.白蚂蚁爬地的路线是AA1→A1D1→‥,黑蚂蚁爬行的路线是AB→BB1→‥,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i![]() N*).设白、黑蚂蚁都走完2020段后各自停止在正方体的某个顶点处,这时黑、白两蚂蚁的距离是( )
N*).设白、黑蚂蚁都走完2020段后各自停止在正方体的某个顶点处,这时黑、白两蚂蚁的距离是( )
A.1B.![]() C.
C.![]() D.0
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆M过点![]() 且与直线
且与直线![]() 相切.
相切.
(1)求动圆圆心M的轨迹C的方程;
(2)斜率为![]() 的直线l经过点
的直线l经过点![]() 且与曲线C交于A,B两点,线段AB的中垂线交x轴于点N,求
且与曲线C交于A,B两点,线段AB的中垂线交x轴于点N,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com