
分析 (1)依题意,可求得等差数列{an}的公差d和等比数列{bn}的公比q的值,继而可求得数列{an}和{bn}的通项公式;
(2)由(1)可求得an=2n-1,bn=2n-1,利用分组求和法可求数列{an-bn}的前n项和Tn.
解答 解:(1)∵数列{an}是首项为1,公差为d的等差数列,
且a1,a2-1,a3-1是等比数列{bn}的前三项,
∴(1+d-1)2=1×(1+2d-1),
∴d=0(舍,否则等比数列{bn}的第二项a2-1=0)或d=2.
an=1+2(n-1)=2n-1;
∴等比数列{bn}的公比q=$\frac{{a}_{2}-1}{{a}_{1}}$=2,又b1=a1=1,
∴bn=2n-1;
(2)∵Tn=(a1-b1)+(a2-b2)+…+(an-bn)
=(a1+a2+…+an)-(b1+b2+…+bn)
=(1+3+5+…+2n-1)-(1+2+22+…+2n-1)
=n2-$\frac{{2}^{n}-1}{2-1}$=n2+1-2n.
点评 本题考查数列的求和,着重考查等差数列与等比数列的通项公式的应用,考查方程思想与分组求和法、公式法的综合应用,属于中档题.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
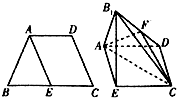 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com