
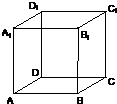
 电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.
电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 26 |
| 81 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 6 |
| 81 |
| 49 |
| 81 |
| X | 0 | 1 | 2 | ||||||
| p |
|
|
|
| 26 |
| 81 |
| 6 |
| 81 |
| 38 |
| 81 |


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
| 5 |
| 2 |
| 1 |
| 2 |
| A、(1)(2)(3) |
| B、(1)(2) |
| C、(1)(3) |
| D、(2)(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 | ||||||||
| 合格的概率 |
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 全月应纳税所得额 | 适用税率(%) | 速算扣除数 |
| 不超过1500元 | 3 | 0 |
| 超过1500元至4500元 | 10 | 105 |
| 超过4500元至9000元 | 20 | 555 |
| … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:
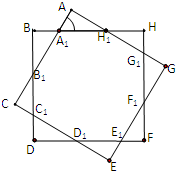 如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设∠AA1H1=α.
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设∠AA1H1=α.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com