Question

20．任取x₁、x₂∈[a，b]，且x₁≠x₂，若f（$\frac{{x}_{1}+{x}_{2}}{2}$）＞$\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$，恒成立，则f（x）称为[a，b]上的凸函数．下列函数中①y=2^x，②y=log₂x，③y=x${\;}^{\frac{1}{2}}$在其定义域上为凸函数是（　　）

• A． ①②
• B． ②③
• C． ①③
• D． ①②③

Answer 1

分析 由凸函数的概念，得出凸函数的几何特征，根据几何特征可作出四个函数①y=2^x，②y=log₂x，③y=x${\;}^{\frac{1}{2}}$的图象，观察图象即可得到答案．

解答 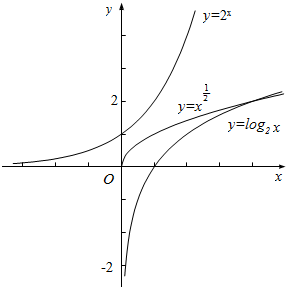解：根据题意：任取x₁，x₂∈[a，b]，且x₁≠x₂，若f（$\frac{{x}_{1}+{x}_{2}}{2}$）＞$\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$，恒成立，f（x）称为[a，b]上的凸函数知：
在函数y=f（x）的图象上任取不同的两点A、B，线段AB（端点除外）总在f（x）图象的上方，则函数f（x）为凸函数，
分别作出四个函数的图象，如图所示．
∴观察①y=2^x，②y=log₂x，③y=x${\;}^{\frac{1}{2}}$在其定义域上的图象，②，③满足凸函数的概念，
故选：B．

点评 本题考查函数的图象，关键在于作出符合凸函数的概念的函数图象，考查数形结合的思想，属于基础题．