
【题目】已知直线l1:3x﹣y﹣1=0,l2:x+2y﹣5=0,l3:x﹣ay﹣3=0不能围成三角形,则实数a的取值可能为( )
A.1B.![]() C.﹣2D.﹣1
C.﹣2D.﹣1
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B. 命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
C. “![]() 在
在![]() 处有极值”是“
处有极值”是“![]() ”的充要条件
”的充要条件
D. 命题“若函数![]() 有零点,则“
有零点,则“![]() 或
或![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.线段![]() 在平面
在平面![]() 内,则直线
内,则直线![]() 不在平面
不在平面![]() 内;B.三条平行直线共面;
内;B.三条平行直线共面;
C.两平面有一个公共点,则一定有无数个公共点;D.空间三点确定一个平面.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一劳动节放假,某商场进行一次大型抽奖活动.在一个抽奖盒中放有红、橙、黄、绿、蓝、紫的小球各2个,分别对应1分、2分、3分、4分、5分、6分.从袋中任取3个小球,按3个小球中最大得分的8倍计分,计分在20分到35分之间即为中奖.每个小球被取出的可能性都相等,用![]() 表示取出的3个小球中最大得分,求:
表示取出的3个小球中最大得分,求:
(1)取出的3个小球颜色互不相同的概率;
(2)随机变量![]() 的概率分布和数学期望;
的概率分布和数学期望;
(3)求某人抽奖一次,中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 离心率等于
离心率等于![]() ,
,![]() 、
、![]() 是椭圆上的两点.
是椭圆上的两点.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.当
两侧的动点.当![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值?如果为定值,请求出此定值;如果不是定值,请说明理由.
的斜率是否为定值?如果为定值,请求出此定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠DAB=60°.
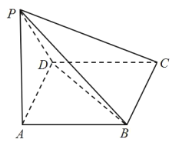
(1)证明:AD⊥PB.
(2)若PB=![]() ,AB=PA=2,求三棱锥P-BCD的体积。
,AB=PA=2,求三棱锥P-BCD的体积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com