
【题目】如图,在△ABC中,∠ACB=![]() ,AC=3, BC=2,P是△ABC内的一点.
,AC=3, BC=2,P是△ABC内的一点.

(1)若△BPC是以BC为斜边的等腰直角三角形,求PA长;
(2)若∠BPC=![]() ,求△PBC面积的最大值.
,求△PBC面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由三角形![]() 为等腰直角三角形,利用勾股定理求出
为等腰直角三角形,利用勾股定理求出![]() 的长,在三角形
的长,在三角形![]() 中,利用余弦定理求出的
中,利用余弦定理求出的![]() 长即可;(2)在三角形
长即可;(2)在三角形![]() 中,由
中,由![]() 的度数表示出
的度数表示出![]() 的度数,利用正弦定理表示出
的度数,利用正弦定理表示出![]() 与
与![]() ,进而表示出三角形
,进而表示出三角形![]() 面积,利用正弦函数的值域确定出面积的最大值即可.
面积,利用正弦函数的值域确定出面积的最大值即可.
(1)由题设,∠PCA=![]() ,PC=
,PC=![]() ,在△PAC中,由余弦定理得
,在△PAC中,由余弦定理得
PA2=AC2+PC2-2AC·PCcos![]() =5,于是PA=
=5,于是PA=![]() .
.
(2)∠BPC=![]() ,设∠PCB=θ,则θ∈(0,
,设∠PCB=θ,则θ∈(0,![]() ).
).
在△PBC中,∠PBC=![]() -θ.由正弦定理得
-θ.由正弦定理得![]() =
=![]() =
=![]() ,
,
得PB=![]() sinθ,PC=
sinθ,PC=![]() sin(
sin(![]() -θ).
-θ).
所以△PBC面积S=![]() PB·PCsin
PB·PCsin![]() =
=![]() sin (
sin (![]() -θ)sinθ=
-θ)sinθ=![]() sin(2θ+
sin(2θ+![]() )-
)-![]() .
.
当θ=![]() ∈(0,
∈(0,![]() )时,△PBC面积的最大值为
)时,△PBC面积的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】数列{an}中,a1=8,a4=2,且满足an+2-2an+1+an=0.
(1)求数列的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如右下表所示(![]() (吨)为买进蔬菜的质量,
(吨)为买进蔬菜的质量,![]() (天)为销售天数):
(天)为销售天数):
(Ⅰ) 根据右表提供的数据在网格中绘制散点图,并判断![]() 与
与![]() 是否线性相关,若线性相关,用最小二乘法求出
是否线性相关,若线性相关,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()

| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅱ)根据(Ⅰ)中的计算结果,若该蔬菜商店准备一次性买进蔬菜25吨,则预计需要销售多少天.
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 (其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(Ⅰ)写出直线l普通方程和曲线C的直角坐标方程;
(Ⅱ)过点M(-1,0)且与直线l平行的直线l1交C于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:①若
有下述四个结论:①若![]() ,则
,则![]() ;②
;②![]() 的图象关于点
的图象关于点![]() 对称;③函数
对称;③函数![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的图象向右平移
的图象向右平移![]() 个单位长度后所得图象关于
个单位长度后所得图象关于![]() 轴对称.其中所有正确结论的编号是( )
轴对称.其中所有正确结论的编号是( )
A.①②④B.①②C.③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,已知曲线![]() ,将曲线
,将曲线![]() 上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线
上的点向左平移一个单位,然后纵坐标不变,横坐标轴伸长到原来的2倍,得到曲线![]() ,又已知直线
,又已知直线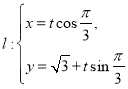 (
(![]() 是参数),且直线
是参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(I)求曲线![]() 的直角坐标方程,并说明它是什么曲线;
的直角坐标方程,并说明它是什么曲线;
(II)设定点![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com