
分析 (1)由f(2)=0,且f(x)=x有两个相等的实数根,求出a、b的值,从而得f(x)的解析式;
(2)根据(1)所求的解析式,判断x∈[1,2]上的单调性,然后求解即可;
(3)根据奇偶函数的定义进行判断和证明.
解答 解:(1)∵f(2)=0,∴4a+2b=0①;
又方程f(x)=x有两个相等的实数根,
即ax2+(b-1)x=0有两个相等的实数根,
∴(b-1)2=0②;
由①②可得,a=-$\frac{1}{2}$,b=1,
∴f(x)=-$\frac{1}{2}$x2+x;
(2)由(1)知f(x)=-$\frac{1}{2}$(x-1)2+$\frac{1}{2}$,
显然函数f(x)在[1,2]上是减函数,
∴x=1时,ymax=$\frac{1}{2}$;x=2时,ymin=0.
∴x∈[1,2]时,函数的值域是[0,$\frac{1}{2}$];
(3)∵F(x)=f(x)-f(-x)+$\frac{m}{{x}^{2}}$=2x+$\frac{m}{{x}^{2}}$,
m=0时,F(x)=2x,∵F(-x)=2(-x)=-2x=-F(x),
∴F(x)是奇函数,
m≠0时,F(x)是非奇非偶函数,不妨取x=1,
得F(-1)=-2+m≠-2-m=-(2+m)=-F(1),
即存在x0=1使得F(-x0)≠-F(x0),
故F(x)是非奇非偶函数.
点评 本题主要考查函数的奇偶性和二次函数在闭区间上的值域问题,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
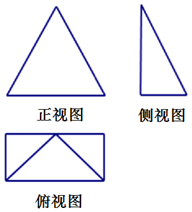 一个空间几何体的三视图如右图,其中正视图是边长为2的正三角形,俯视图是边长分别为1,2的矩形,则该几何体的侧面积为4+$\sqrt{3}$.
一个空间几何体的三视图如右图,其中正视图是边长为2的正三角形,俯视图是边长分别为1,2的矩形,则该几何体的侧面积为4+$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,9) | B. | [-1,9) | C. | [0,9) | D. | (0,9) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com