
在△ABC中,a、b、c分别为角A、B、C所对的边,且(2b+c)cosA十acosC =0。
(1)求角A的大小;
(2)求 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA= acosB.
acosB.
(1)求角B的大小;
(2)若b=3,sinC=2sinA,求a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为绘制海底地貌图,测量海底两点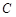 ,
, 间的距离,海底探测仪沿水平方向在
间的距离,海底探测仪沿水平方向在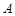 ,
,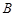 两点进行测量,
两点进行测量,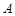 ,
,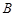 ,
,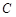 ,
, 在同一个铅垂平面内. 海底探测仪测得
在同一个铅垂平面内. 海底探测仪测得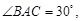

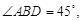
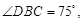
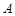 ,
,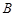 两点的距离为
两点的距离为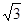 海里.
海里.
(1)求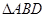 的面积;
的面积;
(2)求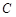 ,
, 之间的距离.
之间的距离.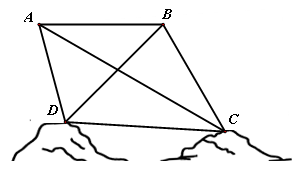
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知a,b,c为△ABC的三个内角A,B,C的对 边,向量m=(
边,向量m=(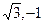 ),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____
),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角B=____▲_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com