���㣺˫���ߵļ�����
ר�⣺�ۺ���,Բ���ߵĶ��塢�����뷽��
��������1���������⣬�ɵæ�
1����
2�Ľ����߷��̣�
��2��˫���ߦ�
1��y=x+
��˫���ߦ�
2��y=x-
�ǹ���˫���ߣ����ù���˫���ߵĶ��������֤���ɣ�
��3���ɣ�2������ֵ��
+
��
���
�⣺��1����
1����
2�Ľ����߷��̷ֱ�Ϊy=x��x=0��
��2��˫���ߦ�
1��y=x+
��˫���ߦ�
2��y=x-
�ǹ���˫���ߣ�֤�����£�
˫���ߦ�
1��y=x+
��ʵ�����ڵ�ֱ����y=x��x=0�Ľ�ƽ��������ֱ��Ϊy=tan67.5��=��
+1��x��
��������ֱ��Ϊy=tan157.5��x=��1-
��x��
ʵ�������Ľ��㵽ԭ��ľ����ƽ��d
2=
a12=2+2
��
��
=tan22.5��=
-1����
b12=2
-2����
c12=4
��
ͬ��˫���ߦ�
2��y=x-
��ʵ�ᡢ�������ڵ�ֱ��y=��1-
��x��y=��
+1��x��
��˫���ߦ�
1��y=x+
��˫���ߦ�
2��y=x-
�ǹ���˫����
��3���ɣ�2��֪
=
��
=
��
��
+
=2����
���������⿼��˫���ߵļ������ʣ������¶��壬���������ʵļ��㣬����ѧ�������������������������е��⣮



 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д� ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
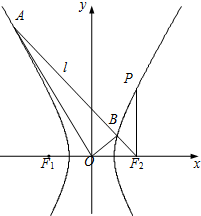 ���P����F1��F2Ϊ���ҽ����˫����C��
���P����F1��F2Ϊ���ҽ����˫����C��