练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

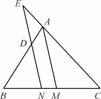
    如图，在△ABC中，作直线DN平行于中线AM，设这条直线交边AB于点D，交边CA的延长线于点E，交边BC于点N.求证：AD∶AB＝AE∶AC.


    证明：∵ AM∥EN，

    ∴ AD∶AB＝NM∶MB，NM∶MC＝AE∶AC.

    ∵ MB＝MC，∴ AD∶AB＝AE∶AC.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知矩阵，在平面直角坐标系中，设直线2x－y＋1＝0在矩阵MN对应的变换作用下得到的曲线F，求曲线F的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     在极坐标系中，圆C的方程为ρ＝2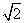sin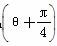，以极点为坐标原点、极轴为x轴正半轴建立平面直角坐标系，直线l的参数方程为 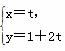(t为参数)，判断直线l和圆C的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中，求曲线ρ＝cosθ＋1与ρcosθ＝1的公共点到极点的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在△ABC中，DE∥BC，DE分别与AB、AC相交于点D、E，若AD＝4，DB＝2，求DE与BC的长度比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在ABCD中，BC＝24，E、F为BD的三等分点，求BM－DN的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     在梯形ABCD中，点E、F分别在腰AB、CD上，EF∥AD，AE∶EB＝m∶n.求证：(m＋n)EF＝mBC＋nAD.

    你能由此推导出梯形的中位线公式吗？

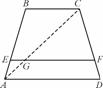
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D.

    (1) 证明：DB＝DC；

    (2) 设圆的半径为1，BC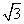＝，延长CE交AB于点F，求△BCF外接圆的半径．

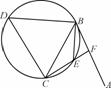
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等比数列{an}满足an＋1＋an＝9·2n－1，n∈N*.

    (1)求数列{an}的通项公式；

    (2)设数列{an}的前n项和为Sn，若不等式Sn＞kan－2对一切n∈N*恒成立，求实数k的取值范围．

    查看答案和解析>>

    同步练习册答案