
分析 画出满足约束条件不等式组$\left\{\begin{array}{l}y≥0\\ y≤x\\ 2x+y-9≤0\end{array}\right.$的平面区域,然后分析平面区域里各个角点,然后将其代入y=a(x+1)中,求出y=a(x+1)对应的a的端点值即可.
解答 解:满足约束条件不等式组$\left\{\begin{array}{l}y≥0\\ y≤x\\ 2x+y-9≤0\end{array}\right.$的平面区域如图示: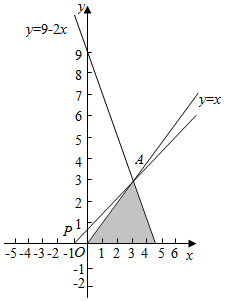
因为y=a(x+1)过定点(-1,0).
所以当y=a(x+1)过点B,由$\left\{\begin{array}{l}{y=x}\\{2x+y-9=0}\end{array}\right.$,解得A(3,3),得到3=a(3+1),解得a=$\frac{3}{4}$,
又因为直线y=a(x+1)与平面区域D有公共点.
所以 0≤a≤$\frac{3}{4}$
故答案为:$[0,\frac{3}{4}]$.
点评 在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
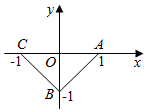
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 年龄(岁) | [20,30) | [30,40) | [40,60) |
| 人数 | 70 | 90 | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 15 | C. | 18 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1) | B. | (-1,1) | C. | (1,2] | D. | (-2,-1)∪(1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com