
分析 解法一:复数z=(a-1)+i,(a∈R)是纯虚数,可得a-1=0,解得a.利用复数的运算法则化简复数$\frac{2+\sqrt{2}i}{a-i}$,再利用模的计算公式即可得出.
解法二:复数z=(a-1)+i,(a∈R)是纯虚数,可得a-1=0,解得a.代入复数$\frac{2+\sqrt{2}i}{a-i}$,利用复数积的模的运算性质即可得出.
解答 解:解法一:复数z=(a-1)+i,(a∈R)是纯虚数,∴a-1=0,解得a=1.
则复数$\frac{2+\sqrt{2}i}{a-i}$=$\frac{2+\sqrt{2}i}{1-i}$=$\frac{(2+\sqrt{2}i)(1+i)}{(1-i)(1+i)}$=$\frac{2-\sqrt{2}+(2+\sqrt{2})i}{2}$,
则复数|$\frac{2+\sqrt{2}i}{a-i}$|=$\sqrt{(\frac{2-\sqrt{2}}{2})^{2}+(\frac{2+\sqrt{2}}{2})^{2}}$=$\sqrt{3}$,
解法二:复数z=(a-1)+i,(a∈R)是纯虚数,∴a-1=0,解得a=1.
则复数$\frac{2+\sqrt{2}i}{a-i}$=$\frac{2+\sqrt{2}i}{1-i}$,
则复数|$\frac{2+\sqrt{2}i}{a-i}$|=$\frac{|2+\sqrt{2}i|}{|1-i|}$=$\frac{\sqrt{{2}^{2}+(\sqrt{2})^{2}}}{\sqrt{2}}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查了复数的有关概念及其运算法则、模的计算公式,考查了推理能力与计算能力,属于中档题.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π:1 | B. | 3π:1 | C. | 2$\sqrt{2}$π:1 | D. | 4π:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | 0 | D. | -11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)设z=$\frac{10i}{3+i}$,则z的共轭复数为?
(1)设z=$\frac{10i}{3+i}$,则z的共轭复数为?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(Х2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
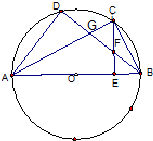 如图,已知AB为圆O的直径,C,D是圆O上的两个点,C是劣弧$\widehat{BD}$的中点,CE⊥AB于E,BD交AC于G,交CE于F.
如图,已知AB为圆O的直径,C,D是圆O上的两个点,C是劣弧$\widehat{BD}$的中点,CE⊥AB于E,BD交AC于G,交CE于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com