
分析 (Ⅰ)利用分段函数的性质求出分段函数的表达式,即可求出f(x)的单调区间;
(Ⅱ)讨论a的取值范围结合函数f(x)有两个零点,构造函数,结合一元二次函数的性质进行求解即可.
解答 解:(Ⅰ)若a=1,f(x)=x2-x|x-1|-k,
若x≥1,则f(x)=x2-x|x-1|-k=x-k,此时函数为增函数,
当x<1时,则f(x)=x2-x|x-1|-k=2x2-x-k=2(x-$\frac{1}{4}$)2-$\frac{1}{8}$-k,
此时在(-∞,$\frac{1}{4}$]为减函数,在[$\frac{1}{4}$,1]上为增函数,
即函数的增区间为[$\frac{1}{4}$,+∞),减区间为(-∞,$\frac{1}{4}$];
(Ⅱ)f(x)=$\left\{\begin{array}{l}{a(x-k),}&{x≥a}\\{2{x}^{2}-ax-ak,}&{x<a}\end{array}\right.$,
当a<0时,
①若x≥a,则由a(x-k)=0,得x1=k>0>a.
②当x<0时,y=2x2-ax-ak在(-∞,$\frac{a}{4}$)上单调递减,且$\frac{a}{4}$>a,
∴y=2x2-ax-ak在(-∞,a)上单调递减,
∴y=2x2-ax-ak>2a2-a2-ak=a2-ak>0,
∴x<0时,2x2-ax-ak=0无解,不满足条件.
当a>0时,①若0<a≤k,
若x≥a,则x-k=0,j即x1-k≥a 是方程f(x)=0的根,
若x<a,令g(x)=2x2-ax-ak,
则g(a)=2a2-a2-ak=a2-ak=a(x-k)<0,
∴在(-∞,a)上存在唯一的x2,使f(x2)=0.
此时|x1-x2|=k-$\frac{a-\sqrt{{a}^{2}+8ak}}{4}$≥k-$\frac{k-\sqrt{{k}^{2}+8{k}^{2}}}{4}$=$\frac{3k}{2}$,
②当a<k时,a(x-k)=0无解,g(a)=a(a-k)>0,
g($\frac{a}{4}$)=$\frac{{a}^{2}}{8}-\frac{{a}^{2}}{4}-ak$=$-\frac{{a}^{2}}{8}-ak$<0,
∴在(-∞,a)上f(x)有两个零点,
此时|x1-x2|=k-$\frac{a-\sqrt{{a}^{2}+8ak}}{4}$>$\frac{3k}{2}$,
综上|x1-x2|=k-$\frac{a-\sqrt{{a}^{2}+8ak}}{4}$≥$\frac{3k}{2}$.
点评 本题主要考查函数单调性和函数零点的应用,根据分段函数的性质是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | ?{0}? | B. | {2} | C. | ?{0,1}? | D. | {-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 121 | B. | 154 | C. | 176 | D. | 352 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
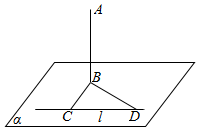 如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.
如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com