
| 用水量(吨) | 单价(元/吨) | 注 |
| 0~20(含) | 2.5 | |
| 20~35(含) | 3 | 超过20吨不超过35吨的部分按3元/吨收费 |
| 35以上 | 4 | 超过35吨的部分按4元/吨收费 |
分析 (Ⅰ)小明家10月份用水量为30吨,在第二档,可得结论;
(Ⅱ)第一档最多为50元,二档最多为50+(35-20)×3元=95元,可得用水量在第三档内,即可得出结论;
(Ⅲ)利用所给条件,即可写出水费y与用水量x之间的函数关系式,并画出函数的图象.
解答 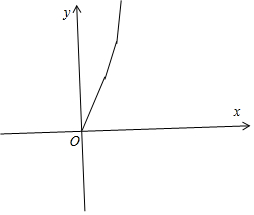 解:(Ⅰ)20×2.5+(30-20)×3=80 …(4分)
解:(Ⅰ)20×2.5+(30-20)×3=80 …(4分)
(Ⅱ)第一档最多为50元
第二档最多为50+(35-20)×3元=95元
∴用水量在第三档内,99-95=4,4÷4=1
∴用水量为35+1=36吨.…(4分)
(Ⅲ)0<x≤20时,f(x)=2.5x;
20<x≤35时,f(x)=20×2.5+(x-20)×3=3x-10;
x>35时,f(x)=20×2.5+(35-20)×3+(x-35)×4=4x-45;
∴f(x)=$\left\{\begin{array}{l}{2.5x,0<x≤20}\\{3x-10,20<x≤35}\\{4x-45,x>35}\end{array}\right.$.
函数的图象如图所示.
点评 本题考查函数分段函数,考查学生利用数学知识解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-2,2) | B. | (-∞,-2)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com