
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
| 3 |
| 1 |
| {an} |
A、3020+
| ||||
B、3020+
| ||||
C、
| ||||
D、3018+
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、简单随机抽样,分层抽样,简单随机抽样 |
| B、系统抽样,系统抽样,简单随机抽样 |
| C、分层抽样,简单随机抽样,简单随机抽样 |
| D、系统抽样,分层抽样,简单随机抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:
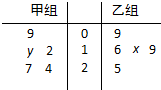 如图茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x,y的值分别为( )
如图茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x,y的值分别为( )| A、7,8 | B、5,7 |
| C、8,5 | D、8,7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
| 2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com