练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若抛物线x=-4y2上一点M到焦点F的距离为1，则点M的横坐标为（　　）
    A、-
    7
    8
    B、-
    9
    8
    C、-
    17
    16
    D、-
    15
    16
    考点：抛物线的简单性质
    专题：计算题,圆锥曲线的定义、性质与方程
    分析：由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，利用抛物线x=-4y2上一点M到焦点F的距离为1，即可求出点M的横坐标．
    解答： 解：∵抛物线x=-4y2，
    ∴
    p
    2
    =
    1
    16
    ，
    ∵抛物线x=-4y2上一点M到焦点F的距离为1，
    ∴由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，
    ∴|MF|=1=
    p
    2
    -x，
    ∴x=-
    15
    16
    ，
    故选：D．
    点评：活用抛物线的定义是解决抛物线问题最基本的方法．抛物线上的点到焦点的距离，叫焦半径．到焦点的距离常转化为到准线的距离求解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知正四棱柱ABCD-A1B1C1D1中AA1=2AB，则CD与平面BDC1所成角的正弦值等于
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题：
    ①函数y=tan
    x
    2
    的图象的对称中心是（kπ，0），k∈Z；
    ②函数y=lg（1+2cos2x）的递减区间是[kπ，kπ+
    π
    4
    ）k∈Z；
    ③函数f（x）=|1+sin2x-cos2x|的最小正周期是π
    ④要得到函数y=sin（
    x
    2
    -
    π
    4
    ）的图象，只需将y=sin
    x
    2
    的图象向右平移
    π
    4
    个单位．
    其中正确的命题序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设函数y=f（x）对任意的x∈R满足f（4+x）=f（-x），当x∈（-∞，2]时，有f（x）=2-x-5．若函数f（x）在区间（k，k+1）（k∈Z）上有零点，则k的值为（　　）
    A、-3或7B、-4或7
    C、-4或6D、-3或6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知：集合P={x|x=sin
    (k-3)π
    3
    ，k∈Z}，集合Q={y|y=sin
    (-21-k)π
    3
    ，k∈Z}，则P与Q的关系是（　　）
    A、P?QB、P?Q
    C、P=QD、P∩Q=∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某奶茶店为了了解奶茶销售量与气温之间的关系，随机统计并制作了6天卖出的奶茶的杯数与气温的对照表：
    气温x（℃） 26 19 14 10 4 -1
    杯数y 201 242 339 383 505 640
    经检验，这组样本数据具有线性相关关系，那么，对于气温x（℃）与奶茶销售量y这两个变量，下列判断正确的是（　　）
    A、成正相关，其回归直线经过点（13，385）
    B、成负相关，其回归直线经过点（13，386）
    C、成正相关，其回归直线经过点（12，386）
    D、成负相关，其回归直线经过点（12，385）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知定义在R上的函数f（x），其导函数y=f′（x）的大致图象如图所示，则下列叙述正确的是（　　）
    A、f（a）取得极小值
    B、f（d）取得最小值
    C、f（x）在（a，c）上单调递增
    D、f（e）取得极大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

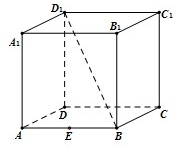    正方体AC1中，E为AB的中点，点P为侧面BB1C1C内一动点（含边界），若动点P始终满足PE⊥BD1，则动点P的轨迹是（　　）
    A、直线B、线段
    C、圆的一部分D、椭圆的一部分

    查看答案和解析>>

    科目：高中数学 来源： 题型：

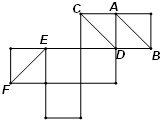    如图是一个正方体纸展开图，如果将它还原成正方体，那么直线AB，CD，EF在原正方体的位置关系是（　　）
    A、AB∥CD，EF⊥CD
    B、AB与CD异面成角60°，CD与EF相交成角60°
    C、AB∥CD，CD与EF相交成角60°
    D、EF⊥CD，AB与CD异面成角60°

    查看答案和解析>>

    同步练习册答案