
| A. | $\frac{{C_{12}^1•C_6^1•C_{20}^1}}{{C_{22}^3-C_{10}^3}}$ | |
| B. | $\frac{{C_{12}^1•C_6^1•C_4^1+C_{12}^1•C_6^2}}{{C_{22}^3-C_{10}^3}}$ | |
| C. | $\frac{{C_{12}^1•(C_6^1•C_4^1+C_6^2)+C_{12}^2•C_6^1}}{{C_{22}^3-C_{10}^3}}$ | |
| D. | $\frac{{C_{22}^3-C_{10}^3-C_{16}^3}}{{C_{22}^3-C_{10}^3}}$ |
分析 先求任选3道题,取到选择题的解法有多少种,然后求任选的3道题中既有选择题又有解答题的选法有多少种,最后带到古典概型的概率公式中即可.
解答 解:从12道选择题、4道填空题、6道解答题中任取3道题取到选择题的取法有${C}_{22}^{3}-{C}_{10}^{3}$中,
其中既取到选择题又取到填空题的情况有两大类,
一是取到一道选择题,此情况的取法有${C}_{12}^{1}({C}_{6}^{1}•{C}_{4}^{1}+{C}_{6}^{2})$种,
二是取到二道选择题,此情况的取法有${C}_{12}^{2}•{C}_{6}^{1}$种,
所以在取到选择题时解答题也取到的概率为$\frac{{C}_{12}^{1}•({C}_{6}^{1}•{C}_{4}^{1}+{C}_{6}^{2})+{C}_{12}^{2}•{C}_{6}^{1}}{{C}_{22}^{3}-{C}_{10}^{3}}$.
故选:C.
点评 本题主要考查古典概型、排列组合等知识,意在考查考生的分类讨论思想和解应用题的能力.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:选择题
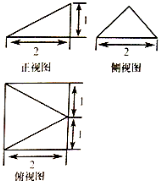
| A. | 4 | B. | $\frac{4}{3}$ | C. | 7+$\sqrt{5}$ | D. | 5+2$\sqrt{2}$+$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2-$\sqrt{3}$,1) | C. | (2-$\sqrt{3}$,2+$\sqrt{3}$) | D. | (1,2+$\sqrt{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com