
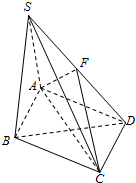
 如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.分析 (1)由题意,三棱锥S-FAC的体积=三棱锥S-DAC的体积的一半,取AB的中点O,连接SA,利用体积公式求三棱锥S-FAC的体积;
(2)求出D到平面AFC的距离,即可求直线BD与平面FAC所成角的正弦值.
解答 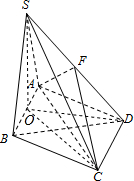 解:(1)由题意,三棱锥S-FAC的体积=三棱锥S-DAC的体积的一半.
解:(1)由题意,三棱锥S-FAC的体积=三棱锥S-DAC的体积的一半.
取AB的中点O,连接SO,则SO⊥底面ABCD,SO=$\sqrt{3}$,
∵S△DAC=$\frac{1}{2}×2×2×sin120°$=$\sqrt{3}$,
∴三棱锥S-FAC的体积=$\frac{1}{3}×\sqrt{3}×\sqrt{3}×\frac{1}{2}$=$\frac{1}{2}$;
(2)连接OD,OC,则OC=OD=$\sqrt{3}$,∴SC=SD=3,
△SAD中,SA=AD=2,F为SD的中点,∴AF=$\sqrt{4-\frac{9}{4}}$=$\frac{\sqrt{7}}{2}$.
△SCD中,SC=SD=3,CD=2,∴9+4CF2=2(9+4),∴CF=$\frac{\sqrt{17}}{2}$,
△FAC中,cos∠AFC=$\frac{\frac{7}{4}+\frac{17}{4}-4}{2×\frac{\sqrt{7}}{2}×\frac{\sqrt{17}}{2}}$=$\frac{6}{\sqrt{119}}$,
∴sin∠AFC=$\sqrt{\frac{83}{119}}$,
∴S△AFC=$\frac{1}{2}$×$\frac{\sqrt{7}}{2}$×$\frac{\sqrt{17}}{2}$×$\sqrt{\frac{83}{119}}$=$\frac{\sqrt{83}}{8}$
设D到平面AFC的距离为h,则$\frac{1}{3}×\frac{\sqrt{83}}{8}h=\frac{1}{2}$,∴h=$\frac{12}{\sqrt{83}}$,
∴直线BD与平面FAC所成角的正弦值$\frac{12}{\sqrt{83}}$÷$\frac{3}{2}$=$\frac{8\sqrt{83}}{83}$
点评 本题考查三棱锥S-FAC的体积,直线BD与平面FAC所成角的正弦值,考查学生的计算能力,正确求体积是关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
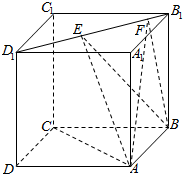 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-∞,3) | C. | (-1,3) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 分层抽样法 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com