练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．一个年级共有12个班，每个班学生的学号从1到50，为交流学习经验，要求每班学号为14的同学留下，这里运用的是（　　）
    A．分层抽样法B．抽签法C．随机数表法D．系统抽样法

    分析 学生人数比较多，把每个班级学生从1到50号编排，要求每班编号为14的同学留下进行交流，这样选出的样本是具有相同的间隔的样本，是采用系统抽样的方法．

    解答 解：当总体容量N较大时，采用系统抽样．将总体分段，分段的间隔要求相等，这时间隔一般为预先制定的，在第1段内采用简单随机抽样确定一个起始编号，在此编号的基础上加上分段间隔的整倍数即为抽样编号．
    本题中，把每个班级学生从1到50号编排，
    要求每班编号为14的同学留下进行交流，
    这样选出的样本是采用系统抽样的方法，
    故选：D．

    点评 本题考查系统抽样，当总体容量N较大时，采用系统抽样，将总体分成均衡的若干部分即将总体分段，分段的间隔要求相等，系统抽样又称等距抽样．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．若α∈（π，2π），且sinα+cosα=$\frac{\sqrt{2}}{4}$．
    （1）求cos2α-cos4α的值； 
    （2）求sinα-cosα的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

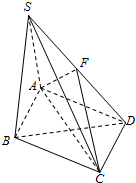    14．如图，在四棱锥S-ABCD中，底面ABCD是菱形，∠BAD=60°，侧面SAB⊥底面ABCD，并且SA=SB=AB=2，F为SD的中点．
    （1）求三棱锥S-FAC的体积；
    （2）求直线BD与平面FAC所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．设命题P：?x∈R，x2-2x＞a，命题Q：?x0∈R，x02+2ax0+2-a=0，如果“P或Q”为真，“P且Q”为假，a的取值范围（-2，-1）∪[1，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．定义：对于函数f（x），若存在非零常数M，T，使函数f（x）对于定义域内的任意实数x，都有f（x+T）-f（x）=M，则称函数f（x）是广义周期函数，其中称T为函数f（x）的广义周期，M称为周距．
    （1）证明函数f（x）=x+（-1）x（x∈Z）是以2为广义周期的广义周期函数，并求出它的相应周距M的值；
    （2）设函数y=g（x）是周期T=2的周期函数（即满足g（x+2）=g（x）），当函数f（x）=-2x+g（x）在[1，3]上的值域为[-3，3]时，求f（x）在[-9，9]上的最大值和最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知直线l：y=2x+2，曲线C：y=lnx+x，直线x=a，（a＞0）交直线l于点A，交曲线C于点B，则|AB|的最小值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．函数$y={log_{\frac{1}{3}}}（3+2x-{x^2}）$的递增区间为（　　）
    A．[1，+∞）B．（-1，1]C．（-∞，1]D．[1，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．极限$\underset{lim}{x→0}$$\frac{1}{2+{3}^{\frac{1}{x}}}$的结果是（　　）
    A．0B．$\frac{1}{2}$C．$\frac{1}{5}$D．不存在

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．设斜率为2的直线l过抛物线y2=2px（p＞0）的焦点F．且与抛物线交于A，B两点．过A，B两点分别作抛物线的准线的垂线，垂足分别为A1，B1，记四边形ABB1A1的面积为S．则$\overrightarrow{AB}•\overrightarrow{{A}_{1}{B}_{1}}$=$\frac{4\sqrt{5}}{5}$S．

    查看答案和解析>>

    同步练习册答案