
分析 (1)把sinα+cosα=$\frac{\sqrt{2}}{4}$两边平方,得到sin$αcosα=-\frac{7}{16}$,由此能求出cos2α-cos4α的值.
(2)由sinαcosα=-$\frac{7}{16}$<0,α∈(π,2π),得sinα<0,cosα>0,先求出(sinα-cosα)2,由此能求出sinα-cosα的值.
解答 解:(1)∵sinα+cosα=$\frac{\sqrt{2}}{4}$,∴(sinα+cosα)2=1+2sinαcosα=$\frac{1}{8}$,
∴sin$αcosα=-\frac{7}{16}$,…..(2分)
∵cos2α-cos4α=cos2α(1-cos2α)=cos2αsin2α=$\frac{49}{256}$.…..(5分)
(2)∵sinαcosα=-$\frac{7}{16}$<0,α∈(π,2π),∴sinα<0,cosα>0,…..(6分)
(sinα-cosα)2=1-2sinαcosα=1+$\frac{7}{8}=\frac{15}{8}$,…..(8分)
∴sinα-cosα=-$\frac{\sqrt{30}}{4}$.…..(10分)
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意同角三角函数关系的合理运用.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:填空题
如果一个正方形的四个项点都在三角形的三边上,则该正方形是该三角形的内接正方形,那么面积为2的锐角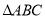 的内接正方形面积的最大值为____________.
的内接正方形面积的最大值为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{27}$ | B. | $-\frac{1}{27}$ | C. | ±$\frac{1}{27}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
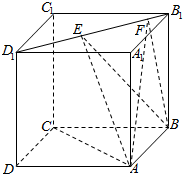 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 分层抽样法 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com