
分析 (1)由题意结合椭圆的定义求得P点的轨迹方程;
(2)假设存在点P(x0,y0),设出P点坐标,利用焦半径公式及勾股定理可得${{x}_{0}}^{2}=50-\frac{625}{{m}^{2}}$.然后结合x0的范围列不等式组求解;
(3)由题意画出图形,求出交点坐标,代入椭圆方程求得m值.
解答 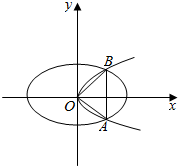 解:(1)动点P到两个定点F1(-m,0),F2(m,0)(0<m<5)的距离之和为10.
解:(1)动点P到两个定点F1(-m,0),F2(m,0)(0<m<5)的距离之和为10.
由题意定义可知,P点轨迹为焦点在x轴上的双曲线,且2a=10,a=5.
又c=m,∴b2=a2-c2=25-m2.
则椭圆方程为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{25-{m}^{2}}=1$;
(2)假设$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{25-{m}^{2}}=1$上存在点Q(x0,y0),使QF1⊥QF2,
则$|Q{F}_{1}|=5+\frac{m}{5}{x}_{0}$,$|Q{F}_{2}|=5-\frac{m}{5}{x}_{0}$.
由QF1⊥QF2,得$(5+\frac{m}{5}{x}_{0})^{2}+(5-\frac{m}{5}{x}_{0})^{2}=4{m}^{2}$.
整理得:${{x}_{0}}^{2}=50-\frac{625}{{m}^{2}}$.
∵${0≤{x}_{0}}^{2}<25$,
∴0$≤50-\frac{625}{{m}^{2}}<25$.
解得:$\frac{5\sqrt{2}}{2}≤m<5$.
∴动点P的轨迹曲线上存在点Q,使QF1⊥QF2,此时实数m的取值范围是[$\frac{5\sqrt{2}}{2},5$);
(3)如图,由题意可得,直线OA的方程为y=$\frac{\sqrt{3}}{3}x$,
联立$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}x}\\{{y}^{2}=x}\end{array}\right.$,解得:B($3,\sqrt{3}$).
把(3,$\sqrt{3}$)代入椭圆$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{25-{m}^{2}}=1$,得$\frac{9}{25}+\frac{3}{25-{m}^{2}}=1$.
解得:$m=\frac{5\sqrt{15}}{4}$.
点评 本题考查椭圆标准方程的求法,考查了椭圆的简单性质,训练了椭圆焦半径公式的应用,考查了椭圆与抛物线的位置关系,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
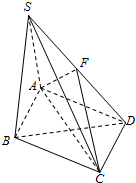 如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,∠BAD=60°,侧面SAB⊥底面ABCD,并且SA=SB=AB=2,F为SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-1,1] | C. | (-∞,1] | D. | [1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{5}$ | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α⊥γ,α⊥β,则γ∥β | B. | 若m∥n,m?α,n?β,则α∥β | ||
| C. | 若m∥n,m⊥α,n⊥β,则α∥β | D. | 若m∥n,m∥α,则n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{3}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com