
分析 求得g(x)=ex,设过原点的切线方程为y=kx,与y=lnx的切点为(m,lnm),与y=g(ax)的切点为(n,ean),由导数的几何意义和斜率公式,得到方程组,解方程即可得到所求a的值.
解答 解:函数f(x)=lnx,曲线y=g(x)与曲线y=f(x)关于直线y=x对称,
可得g(x)=ex,
设过原点的切线方程为y=kx,
与y=lnx的切点为(m,lnm),与y=g(ax)的切点为(n,ean),
由y=lnx的导数y′=$\frac{1}{x}$,y=eax的导数y′=aeax,
即有k=$\frac{1}{m}$=aean=$\frac{lnm}{m}$=$\frac{{e}^{an}}{n}$,
解得m=e,k=$\frac{1}{e}$,n=e2,an=1,则a=$\frac{1}{n}$=$\frac{1}{{e}^{2}}$.
故答案为:$\frac{1}{{e}^{2}}$.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义,注意设出切点和正确求导是解题的关键,考查运算求解能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 微信群数量(个) | 频数 | 频率 |
| 0~4 | 0.15 | |
| 5~8 | 40 | 0.4 |
| 9~12 | 25 | |
| 13~16 | a | c |
| 16以上 | 5 | b |
| 合计 | 100 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
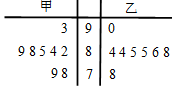 某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )| A. | 甲、乙生产的零件尺寸的中位数相等 | |
| B. | 甲、乙生产的零件质量相当 | |
| C. | 甲生产的零件质量比乙生产的零件质量好 | |
| D. | 乙生产的零件质量比甲生产的零件质量好 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com