
【题目】已知函数![]() .
.
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)构造函数![]() ,对函数
,对函数![]() 求导,从而得到函数
求导,从而得到函数![]() 的最大值,则不等式获证;(2)先对函数
的最大值,则不等式获证;(2)先对函数![]() 求导,再对参数
求导,再对参数![]() 分类讨论,分别求得函数
分类讨论,分别求得函数![]() 在
在![]() 上的最大值,将不等式恒成立问题转化为
上的最大值,将不等式恒成立问题转化为![]() 的最大值小于或等于0,即可得到实数
的最大值小于或等于0,即可得到实数![]() 的取值范围.
的取值范围.
解:(1)易知函数![]() 的定义域为
的定义域为![]() .
.
设![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 处取得最大值,
处取得最大值,
所以![]() ,
,
所以![]() .
.
(2)因为![]() ,所以
,所以![]() .
.
①当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() ,所以
,所以![]() 满足题意.
满足题意.
②当![]() 时,令
时,令![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 处取得最大值.
处取得最大值.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() ,不符合题意.
,不符合题意.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() .
.
设![]() ,则
,则![]() .
.
当 时,
时,![]() ,所以
,所以![]() 在
在 上单调递增,
上单调递增,
所以当 时,
时,![]() ,不满足题意.
,不满足题意.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() ,所以
,所以![]() 满足题意.
满足题意.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是等边三角形,
的底面是等边三角形,![]() 在底面ABC上的射影为△ABC的重心G.
在底面ABC上的射影为△ABC的重心G.
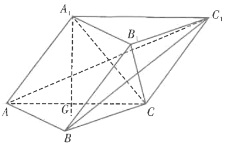
(1)已知![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)已知平面![]() 与平面ABC所成的二面角为60°,G到直线AB的距离为a,求锐二面角
与平面ABC所成的二面角为60°,G到直线AB的距离为a,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过椭圆![]() 的四个顶点与坐标轴垂直的四条直线围成的矩形
的四个顶点与坐标轴垂直的四条直线围成的矩形![]() (
(![]() 是第一象限内的点)的面积为
是第一象限内的点)的面积为![]() ,且过椭圆
,且过椭圆![]() 的右焦点
的右焦点![]() 的倾斜角为
的倾斜角为![]() 的直线过点
的直线过点![]() .
.
(1)求椭圆![]() 的标准方程
的标准方程
(2)若射线![]() 与椭圆
与椭圆![]() 的交点分别为
的交点分别为![]() .当它们的斜率之积为
.当它们的斜率之积为![]() 时,试问
时,试问![]() 的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出此定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国剪纸是我国广大劳动人民在生产与生活实践中创造出来的一种平面剪刻艺术.民间剪纸艺术是我国优秀的非物质文化遗产之一,在千百年的发展过程中,积淀了丰厚的文化历史,取得了卓越的艺术成就.2020年3月发行的邮票《中国剪纸(二)》共4枚,第一枚邮票《三娘教子》(如图1)出自“孟母教子”的故事,讲述了母亲通过断织等行为教育孩子努力上进,懂得感恩.图2是某剪纸艺术家根据第一枚邮票用一张半径为4个单位的圆形纸片裁剪而成的《三娘教子》剪纸.为了测算图2中有关部分的面积,在圆形区域内随机投掷400个点,其中落入图案上的点有225个,据此可估计剪去部分纸片的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解运动健身减肥的效果,某健身房调查了20名肥胖者,测量了他们的体重(单位:千克).健身之前他们的体重情况如三维饼图(1)所示,经过半年的健身后,他们的体重情况如三维饼图(2)所示,对比健身前后,关于这20名肥胖者,下面结论正确的是( )
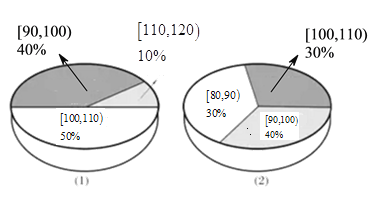
A.他们健身后,体重在区间![]() 内的人数不变
内的人数不变
B.他们健身后,体重在区间![]() 内的人数减少了2个
内的人数减少了2个
C.他们健身后,体重在区间![]() 内的肥胖者体重都有减轻
内的肥胖者体重都有减轻
D.他们健身后,这20位肥胖着的体重的中位数位于区间![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,点![]() 在曲线
在曲线![]() 上,直线l过点
上,直线l过点![]() 且与OM垂直,垂足为P.
且与OM垂直,垂足为P.
(1)当![]() 时,求在直角坐标系下点
时,求在直角坐标系下点![]() 坐标和l的方程;
坐标和l的方程;
(2)当M在C上运动且P在线段OM上时,求点P在极坐标系下的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com