
分析 (1)求得f(x)=-x3+mx2-m,求出导数,讨论当$\frac{2m}{3}$≥6即9≤m<20时,当2<$\frac{2m}{3}$<6,即为3<m<9时,当$\frac{2m}{3}$≤2,即0<m≤3时,可得f(x)的单调性;
(2)求出f(x)的导数,可得A,B处的切线方程,代入点(2,-lga),可得x1,x2为方程-lga-(-x3+mx2-m)=(-3x2+2mx)(2-x)的两个不等实根,化简整理可得,2x3-(m+6)x2+4mx-m+lga=0,令g(x)=2x3-(m+6)x2+4mx-m+lga,求出导数和极值点,由题意可得g(x)必有一个极值为0,对m讨论,结合a≥1,解不等式即可得到所求m的范围.
解答 解:(1)函数f($\frac{x}{2}$)=-$\frac{1}{8}$x3+$\frac{m}{4}$x2-m,
可得f(x)=-x3+mx2-m,
f′(x)=-3x2+2mx=-x(3x-2m),
当$\frac{2m}{3}$≥6即9≤m<20时,函数f(x)在区间[2,6]上的单调递增;
当2<$\frac{2m}{3}$<6,即为3<m<9时,f(x)在[2,$\frac{2m}{3}$)递增,在($\frac{2m}{3}$,6]递减;
当$\frac{2m}{3}$≤2,即0<m≤3时,函数f(x)在区间[2,6]上的单调递减;
(2)f′(x)=-3x2+2mx,可得A处的切线方程:y-(-x13+mx12-m)=(-3x12+2mx)(x-x1),
同理可得B处的切线方程:y-(-x23+mx22-m)=(-3x22+2mx)(x-x2),
代入点(2,-lga),可得x1,x2为方程-lga-(-x3+mx2-m)=(-3x2+2mx)(2-x)的两个不等实根,
化简整理可得,2x3-(m+6)x2+4mx-m+lga=0,
令g(x)=2x3-(m+6)x2+4mx-m+lga,g′(x)=6x2-2(m+6)x+4m=2(3x-m)(x-2),
由0<m<20,可得g′(x)=0,可得x=2或x=$\frac{m}{3}$.
g(2)=3m-8+lga,g($\frac{m}{3}$)=-$\frac{1}{27}$m3+$\frac{2}{3}$m2-m+lga,
由题意可得g(x)必有一个极值为0,
(Ⅰ)若$\frac{1}{3}$m<2,即0<m<6,由g(2)=0,g($\frac{m}{3}$)>0,
可得lga=8-3m≥0,即m≤$\frac{8}{3}$,
则g($\frac{m}{3}$)=-$\frac{1}{27}$m3+$\frac{2}{3}$m2-m+8-3m=-$\frac{1}{27}$(m-6)3>0成立,
即有0<m≤$\frac{8}{3}$;①
由g(2)<0,g($\frac{m}{3}$)=0,
可得lga+3m-8<0,-$\frac{1}{27}$m3+$\frac{2}{3}$m2-m+lga=0,
由lga≥0,可得0≤m≤9-3$\sqrt{6}$或m≥9+3$\sqrt{6}$,
由g(2)=$\frac{1}{27}$m3-$\frac{2}{3}$m2+m-8+3m=$\frac{1}{27}$(m-6)3<0,
解得m<6,即有0<m≤9-3$\sqrt{6}$;②
(Ⅱ)若$\frac{1}{3}$m>2,即6<m<20,由g(2)=0,g($\frac{m}{3}$)<0,
可得lga=8-3m≥0,即m≤$\frac{8}{3}$,
则m无解;③
由g(2)>0,g($\frac{m}{3}$)=0,
可得lga+3m-8>0,-$\frac{1}{27}$m3+$\frac{2}{3}$m2-m+lga=0,
由lga≥0,可得0≤m≤9-3$\sqrt{6}$或m≥9+3$\sqrt{6}$,
由g(2)=$\frac{1}{27}$m3-$\frac{2}{3}$m2+m-8+3m=$\frac{1}{27}$(m-6)3>0,
解得m>6,即有9+3$\sqrt{6}$≤m<20,④
综上可得,0<m≤$\frac{8}{3}$或9+3$\sqrt{6}$≤m<20.
点评 本题考查导数的运用:求单调性和切线方程,注意运用分类讨论的思想方法和转化思想的运用,考查化简整理的运算能力,综合性强,具有一定的难度.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:选择题
设奇函数f(x)在(0,+∞)上是增函数,且f(1)=0,则不等式x[f(x)-f(-x)]<0的解集为 ( )
A.{x|-1<x<0或x>1} B.{x|x<-1或0<x<1}
C.{x|x<-1或x>1} D.{x|-1<x<0或0<x<1}
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:选择题
若函数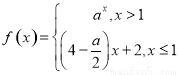 是R上的单调递增函数,则实数a的取值范围为( )
是R上的单调递增函数,则实数a的取值范围为( )
A.(1,+∞) B.(1,8) C.(4,8) D.[4,8)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α且n∥α,则m∥n | B. | 若m⊥β且m⊥n,则n∥β | ||
| C. | 若m⊥α且m∥β,则α⊥β | D. | 若m不垂直于α,且n?α则m不垂直于n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$-1 | D. | $\sqrt{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com