
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
分析 根据题意,用特殊值代入计算,即可判断命题是否正确.
解答 解:【特殊值法】a>b>0,ab=ba,
不妨令a=4,b=2,满足条件;
则a=4>e,b=2<e,①正确,②错误;
又ab=2×4>e2,④正确,③错误;
综上,正确的命题是①④.
【直接法】a>b>0,ab=ba,
∴blna=alnb,
∴$\frac{lna}{a}$=$\frac{lnb}{b}$;
设f(x)=$\frac{lnx}{x}$(x>0),
则f′(x)=$\frac{1-lnx}{{x}^{2}}$,
令f′(x)=0,得1-lnx=0,解得x=e;
∴x∈(0,e)时,f′(x)>0,f(x)是增函数;
x∈(e,+∞)时,f′(x)<0,f(x)是减函数;
∴x=e时f(x)取得最大值为f(e)=$\frac{1}{e}$;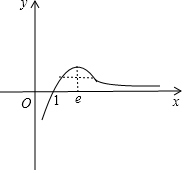
由函数的图象知,a、b中a>e,1<b<e,∴①正确,②错误;
由$\frac{lna}{a}$=$\frac{lnb}{b}$=k>0,
∴$\left\{\begin{array}{l}{lna=at①}\\{lnb=bt②}\end{array}\right.$
①-②得$\frac{lna-lnb}{a-b}$=t
①+②得lna+lnb=t(a+b)=$\frac{ln\frac{a}{b}(a+b)}{a-b}$=$\frac{(\frac{a}{b}+1)ln\frac{a}{b}}{\frac{a}{b}-1}$
lna+lnb-2=$\frac{(\frac{a}{b}+1)ln\frac{a}{b}}{\frac{a}{b}-1}$-2③
令u=$\frac{a}{b}$,则③式变为
lna+lnb-2=$\frac{(u+1)lnu}{u-1}$-2=$\frac{u+1}{u-1}$(lnu-$\frac{2(u-1)}{u+1}$)
∵a>e,1<b<e,∴u∈(0,1)
另f(u)=lnu-$\frac{2(u-1)}{u+1}$
∵f′(u)=$\frac{1}{u}$-$\frac{4}{(u+1)^{2}}$<0,∴f(u)在(0,1)上单调递减,f(u)<0,
由∵u-1<0,
∴lna-lnb>2
∴a•b>e2,③错误,④正确.
综上,正确结论的序号是①④.
故选:C.
点评 本题考查了用特殊值判断数值大小的应用问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤-2 | B. | -2≤m≤0 | C. | 0≤m≤2 | D. | m≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $[{0,\frac{{\sqrt{3}}}{3}})$ | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $[{0,\sqrt{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (4,+∞) | C. | (0,4) | D. | (-∞,0)∪(4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com