
分析 (1)由题意可得:ex=g(x)+h(x),e-x=g(-x)+h(-x)=g(x)-h(x),联立解得:g(x),h(x).由y=$\frac{{e}^{x}-{e}^{-x}}{2}$,化为:(ex)2-2yex-1=0,ex>0,解得ex=y+$\sqrt{{y}^{2}+1}$.可得h-1(x).
(2)φ(x)=g(x-1),函数φ(x)在[-1,3]上满足φ(2a+1>φ(-$\frac{a}{2}$),转化为:函数g(x)在[-2,2]上满足:g(2a)>g(-$\frac{a}{2}$-1),由于函数g(x)在[0,+∞)上单调递增,且函数g(x)为偶函数,可得|2a|>|-$\frac{a}{2}$-1|,-2≤2a≤2,-2≤-$\frac{a}{2}$-1≤2,解得a范围.
(3)不等式g(2x)-ah(x)≥0,即$\frac{{e}^{2x}+{e}^{-2x}}{2}$-$a×\frac{{e}^{x}-{e}^{-x}}{2}$≥0,令t=ex-e-x,由x∈(0,2],可得t∈(0,e2-e-2],不等式转化为:t2+2-at≥0,a≤t+$\frac{2}{t}$,利用基本不等式的性质即可得出.
解答 解:(1)由题意可得:ex=g(x)+h(x),e-x=g(-x)+h(-x)=g(x)-h(x),
联立解得:g(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,h(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$.
由y=$\frac{{e}^{x}-{e}^{-x}}{2}$,化为:(ex)2-2yex-1=0,ex>0,解得ex=y+$\sqrt{{y}^{2}+1}$.
∴h-1(x)=ln$(x+\sqrt{{x}^{2}+1})$(x∈R).
(2)φ(x)=g(x-1),函数φ(x)在[-1,3]上满足φ(2a+1>φ(-$\frac{a}{2}$),
转化为:函数g(x)在[-2,2]上满足:g(2a)>g(-$\frac{a}{2}$-1),
由于函数g(x)在[0,+∞)上单调递增,且函数g(x)为偶函数,
∴|2a|>|-$\frac{a}{2}$-1|,-2≤2a≤2,-2≤-$\frac{a}{2}$-1≤2,解得a∈$[-1,-\frac{2}{5})$∪$(\frac{2}{3},1]$.
(3)不等式g(2x)-ah(x)≥0,即$\frac{{e}^{2x}+{e}^{-2x}}{2}$-$a×\frac{{e}^{x}-{e}^{-x}}{2}$≥0,
令t=ex-e-x,由x∈(0,2],可得t∈(0,e2-e-2],
不等式转化为:t2+2-at≥0,∴a≤t+$\frac{2}{t}$,∵t+$\frac{2}{t}$≥2$\sqrt{2}$,当且仅当t=$\sqrt{2}$时取等号.
∴a≤2$\sqrt{2}$.
点评 本题考查了指数函数与对数的运算性质及其函数的单调性、函数的奇偶性、不等式的解法、基本不等式的性质,考查了推理能力与计算能力,属于难题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$-1 | D. | $\sqrt{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0\;,\;\frac{{\sqrt{7}}}{7})$ | B. | $(\frac{{\sqrt{7}}}{7}\;,\;1)$ | C. | $(\frac{{\sqrt{5}}}{5}\;,\;1)$ | D. | $(\frac{{\sqrt{7}}}{7}\;,\;\frac{{\sqrt{5}}}{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
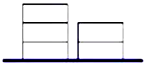 如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).
如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 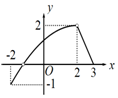 | B. |  | C. |  | D. | 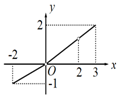 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向左平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com