
| A. | $(0\;,\;\frac{{\sqrt{7}}}{7})$ | B. | $(\frac{{\sqrt{7}}}{7}\;,\;1)$ | C. | $(\frac{{\sqrt{5}}}{5}\;,\;1)$ | D. | $(\frac{{\sqrt{7}}}{7}\;,\;\frac{{\sqrt{5}}}{5})$ |
分析 由已知的偶函数f(x)的定义域为R,且f(1+x)=f(1-x),得到函数的对称轴为x=1并且周期为2,在同一个坐标系中画出f(x)以及y=$lo{g}_{m}\frac{1}{x+2}$的图象,由在x∈[0,5]上有4个不相等的实数根得到函数图象交点为4个的时候对应的m 的范围.
解答 解:因为偶函数f(x)的定义域为R,且f(1+x)=f(1-x),所以f(1+x)=f(x-1),得到函数的正确为2,且关于x=n,n∈N对称,函数f(x)以及y=log${\;}_{m}\frac{1}{x+2}$=-logm(x+2)的图象如图,要使关于x的方程$f(x)-{log_m}\frac{1}{x+2}=0$在x∈[0,5]上有4个不相等的实数根,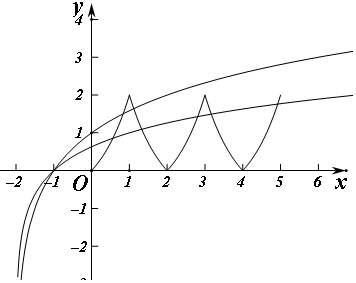 只要$\left\{\begin{array}{l}{0<m<1}\\{-lo{g}_{m}(5+2)>{3}^{5-4}-1}\\{-lo{g}_{m}(3+2)<{3}^{3-2}-1}\end{array}\right.$
只要$\left\{\begin{array}{l}{0<m<1}\\{-lo{g}_{m}(5+2)>{3}^{5-4}-1}\\{-lo{g}_{m}(3+2)<{3}^{3-2}-1}\end{array}\right.$
解得$\frac{\sqrt{7}}{7}<m<\frac{\sqrt{5}}{5}$;
即实数m的取值范围是($\frac{\sqrt{7}}{7},\frac{\sqrt{5}}{5}$);
故选:D.
点评 本题考查了利用函数图象的交点求方程根的个数问题;正确画图并且识图是关键.


科目:高中数学 来源: 题型:解答题
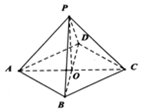 如图,在边长为2的菱形ABCD中,∠BAD=60°,O为AC的中点,点P为平面ABCD外一点,且平面PAC⊥平面ABCD,PO=1,PA=2.
如图,在边长为2的菱形ABCD中,∠BAD=60°,O为AC的中点,点P为平面ABCD外一点,且平面PAC⊥平面ABCD,PO=1,PA=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=(0,1,-1),$\overrightarrow{b}$=(1,0,-1) | B. | $\overrightarrow{a}$=(1,-1,1),$\overrightarrow{b}$=(-1,0,1) | ||
| C. | $\overrightarrow{a}$=(0,1,-2),$\overrightarrow{b}$=(0,-2,2) | D. | $\overrightarrow{a}$=(1,-1,1),$\overrightarrow{b}$=(-1,1,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤-2 | B. | -2≤m≤0 | C. | 0≤m≤2 | D. | m≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $[{0,\frac{{\sqrt{3}}}{3}})$ | C. | $[{-\sqrt{3},\sqrt{3}}]$ | D. | $[{0,\sqrt{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com