
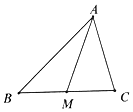
 如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.
如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.分析 (Ⅰ)根据向量的加法以及中点的定义求出$\overrightarrow{AM}$即可;
(Ⅱ)求出∠BAC的余弦值,从而求出AM的长即可.
解答 解:(Ⅰ)∵M是BC的中点
∴$\overrightarrow{AM}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$)=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$);
(Ⅱ)∵sin∠BAC=$\frac{4}{5}$,△ABC是锐角三角形,
∴cos∠BAC=$\frac{3}{5}$,
∴${|\overrightarrow{AM}|}^{2}$=$\frac{1}{4}$(${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$)=$\frac{1}{4}$(25+2×5×3×$\frac{3}{5}$+9)=13,
∴|$\overrightarrow{AM}$|=$\sqrt{13}$,即中线AM=$\sqrt{13}$.
点评 本题考查平面向量基本定理,模的几何意义,简单题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相切 | B. | 相交 | C. | 相离 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
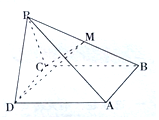 如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.
如图,在棱锥P-ABCD中,侧面PDC是边长为2的正三角形,底面ABCD是菱形,平面PCD⊥平面ABCD,M是PB的中点,且∠BCD=120°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某货运公司规定,从甲城到乙城的计价标准是:40吨以内100元(含40吨),超出40吨的部分4元/吨.
某货运公司规定,从甲城到乙城的计价标准是:40吨以内100元(含40吨),超出40吨的部分4元/吨.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com