
(本小题满分14分)已知函数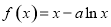 ,
,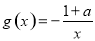 (
(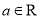 ).
).
(1)若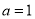 ,求函数
,求函数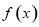 的极值;
的极值;
(2)设函数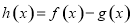 ,求函数
,求函数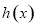 的单调区间;
的单调区间;
(3)若在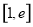 (
(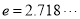 )上存在一点
)上存在一点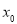 ,使得
,使得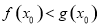 成立,求
成立,求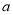 的取值范围.
的取值范围.
(1)当 时,函数
时,函数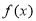 取得极小值1;(2)当
取得极小值1;(2)当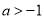 时,
时,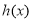 的递减区间为
的递减区间为 ;递增区间为
;递增区间为 ,当
,当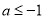 时,
时, 只有递增区间为
只有递增区间为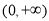 ;(3)
;(3)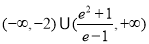 .
.
【解析】
试题分析:本题主要考查导数的运算、利用导数判断函数的单调区间、利用导数求函数的极值和最值等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,当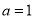 时,先得到
时,先得到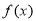 解析式,在定义域范围内,解不等式
解析式,在定义域范围内,解不等式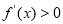 ,
, 得到函数的单调区间,从而得到函数
得到函数的单调区间,从而得到函数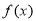 的极值;第二问,先求出
的极值;第二问,先求出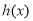 表达式,对
表达式,对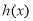 求导,需讨论
求导,需讨论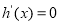 的根
的根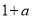 与0的大小,分情况讨论;第三问,将在
与0的大小,分情况讨论;第三问,将在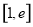 (
(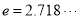 )上存在一点
)上存在一点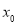 ,使得
,使得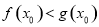 成立转化为
成立转化为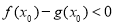 ,构造函数
,构造函数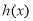 ,结合第二问的结论,讨论求
,结合第二问的结论,讨论求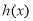 的最小值.
的最小值.
试题解析:(1)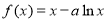 的定义域为
的定义域为 . 1分
. 1分
当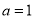 时,
时,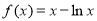 ,
,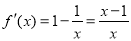 . 2分
. 2分
由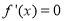 ,解得
,解得 .
.
当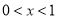 时,
时,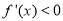 ,
,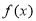 单调递减;
单调递减;
当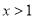 时,
时,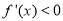 ,
,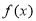 单调递增;
单调递增;
所以当 时,函数
时,函数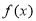 取得极小值,极小值为
取得极小值,极小值为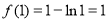 ; 4分
; 4分
(2)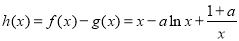 ,其定义域为
,其定义域为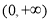 .
.
又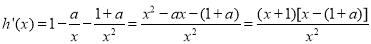 . 5分
. 5分
①当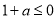 ,即
,即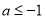 时,在
时,在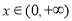 上
上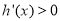 ,所以,函数
,所以,函数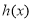 在
在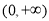 上单调递增. 6分
上单调递增. 6分
②当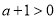 ,即
,即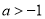 时,在
时,在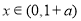 上
上 ,在
,在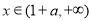 上
上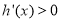 ,
,
所以 在
在 上单调递减,在
上单调递减,在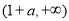 上单调递增; 7分
上单调递增; 7分
综上所述:当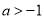 时,
时,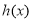 的递减区间为
的递减区间为 ;递增区间为
;递增区间为 .
.
当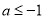 时,
时, 只有递增区间为
只有递增区间为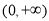 . 8分
. 8分
(3)若在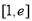 上存在一点
上存在一点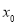 ,使得
,使得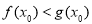 成立,即在
成立,即在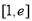 上存在一点
上存在一点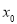 ,使得
,使得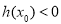 .
.
则函数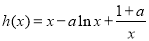 在
在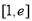 上的最小值小于零. 9分
上的最小值小于零. 9分
①当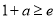 ,即
,即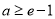 时,由(2)可知
时,由(2)可知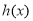 在
在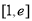 上单调递减.
上单调递减.
故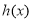 在
在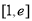 上的最小值为
上的最小值为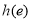 ,由
,由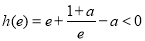 ,可得
,可得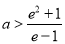 .
.
因为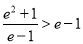 .所以
.所以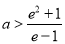 ; 10分
; 10分
②当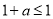 ,即
,即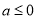 时,由(2)可知
时,由(2)可知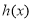 在
在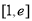 上单调递增.
上单调递增.
故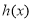 在
在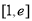 上最小值为
上最小值为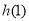 ,由
,由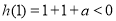 ,
,
可得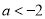 (满足
(满足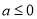 ); 11分
); 11分
③当 ,即
,即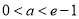 时,由(2)可知可得
时,由(2)可知可得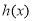 在
在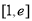 上最小值为
上最小值为
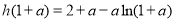 .
.
因为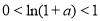 ,所以,
,所以,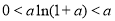 .
.

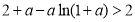 ,即
,即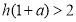 不满足题意,舍去. 13分
不满足题意,舍去. 13分
综上所述得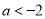 ,或
,或 .
.
 实数
实数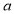 的取值范围为
的取值范围为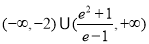 . 14分
. 14分
考点:导数的运算、利用导数判断函数的单调区间、利用导数求函数的极值和最值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年黑龙江省绥化市高三下学期期初开学联考理科数学试卷(解析版) 题型:选择题
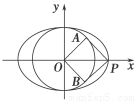
已知椭圆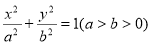 ,以O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A、B,若四边形PAOB为正方形,则椭圆的离心率为( )
,以O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A、B,若四边形PAOB为正方形,则椭圆的离心率为( )
A.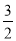 B.
B.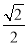 C.
C.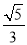 D.
D.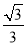
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省潮州市高三上学期期末教学质量检测文科数学试卷(解析版) 题型:选择题
高三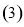 班共有学生
班共有学生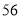 人,现根据座号,用系统抽样的方法,抽取一个容量为
人,现根据座号,用系统抽样的方法,抽取一个容量为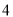 的样本.已知
的样本.已知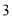 号、
号、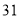 号、
号、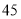 号同学在样本中,那么样本中还有一个同学的座号是( )
号同学在样本中,那么样本中还有一个同学的座号是( )
A.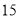 B.
B.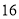 C.
C.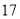 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省潮州市高三上学期期末教学质量检测理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数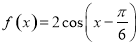 ,
,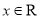 .
.
(1)求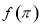 的值;
的值;
(2)若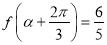 ,
,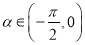 ,求
,求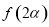 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省潮州市高三上学期期末教学质量检测理科数学试卷(解析版) 题型:选择题
若函数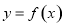 (
(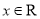 )满足
)满足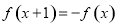 ,且
,且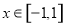 时,
时,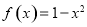 ,已知函数
,已知函数 ,则函数
,则函数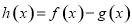 在区间
在区间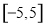 内的零点的个数为( )
内的零点的个数为( )
A.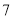 B.
B.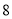 C.
C.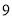 D.
D.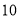
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省、湘阴县一中高三12月联考理科数学试卷(解析版) 题型:填空题
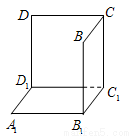
如图是从上下底面处在水平状态下的棱长为1m的正方体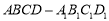 中分离出来的.如果用图示中这样一个装置来盛水,那么最多能盛
中分离出来的.如果用图示中这样一个装置来盛水,那么最多能盛 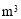 体积的水.
体积的水.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com