
分析 先根据关于t的函数,利用判别式,再分离参数,利用基本不等式即可求出答案.
解答 解:∵不等式mt2+$\sqrt{xy+yz}$t+x2+2y2+3z2≥0恒成立,
∴△≤0,
即(xy+yz)-4m(x2+2y2+3z2)≤0,
∴m≥$\frac{1}{4}$•$\frac{xy+yz}{{x}^{2}+2{y}^{2}+3{z}^{2}}$恒成立,
∵x2+2y2+3z2=(x2+$\frac{3}{2}$y2)+($\frac{1}{2}$y2+3z2)≥2$\sqrt{\frac{3}{2}}$(xy+yz)=$\sqrt{6}$(xy+yz),
∴$\frac{xy+yz}{{x}^{2}+2{y}^{2}+3{z}^{2}}$≤$\frac{\sqrt{6}}{6}$,
∴m≥$\frac{\sqrt{6}}{24}$,
故答案为:($\frac{\sqrt{6}}{24}$,+∞)
点评 本题考查了恒成立的问题,关键是分离参数,构造基本不等式,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,斜截圆柱的截面是一个椭圆,则该椭圆的焦距为30cm.
在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长最短50cm,最长80cm,斜截圆柱的截面是一个椭圆,则该椭圆的焦距为30cm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届辽宁庄河市高三9月月考数学(文)试卷(解析版) 题型:解答题
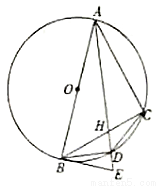
选修4-1:几何证明选讲
如图,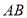 是
是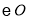 的直径,
的直径,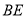 为
为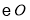 的切线,点
的切线,点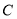 为
为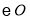 上不同于
上不同于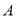 、
、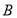 的一点,
的一点,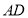 为
为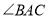 的平分线,且分别与
的平分线,且分别与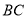 交于
交于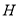 ,与
,与 交于
交于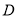 ,与
,与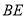 交于
交于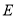 ,连接
,连接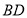 、
、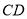 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求证: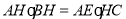 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com