
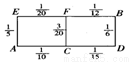
(本题14分)张老师居住在某城镇的A处,准备开车到学校B处上班。若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图。(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为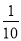 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为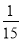 )。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量
)。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量 ,求
,求 的数学期望
的数学期望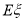 。
。
(1)路线A→C→F→B,可使得途中发生堵车事件的概率最小;(2) 。
。
【解析】
试题分析:(1)分别求出路线A→C→D→B、路线A→E→F→B、A→C→F→B遇到堵车的概率,比较求出其中最小的, 以路线A→C→D→B遇到堵车的概率为例,可先求出路线A→C→D→B没有遇到堵车的概率;(2)路线A→C→F→B中遇到堵车次数 可取值为0,1,2,3,
可取值为0,1,2,3,
 =0时,没有堵车;
=0时,没有堵车; =1时,有一段堵车,;
=1时,有一段堵车,; =2时,,有两段堵车;
=2时,,有两段堵车; =3时,三段均堵车,期望
=3时,三段均堵车,期望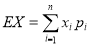 求出即可.
求出即可.
试题解析:(1)记路段AC发生堵车事件为AC,其余同此表示法。因为各路段发生堵车事件是独立的,且在同一路段发生堵车事件最多只有一次,所以路线A→C→D→B中遇到堵车的概率P1为
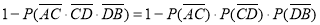
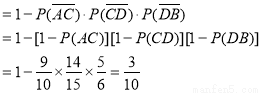
同理:路线A→C→F→B中遇到堵车的概率P2为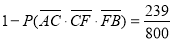
路线A→E→F→B中遇到堵车的概率P3为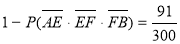
显然要使得A到B的路线途中发生堵车事件的概率最小,只可能在以上三条路线中选择。又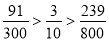
因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小
(2)路线A→C→F→B中遇到堵车次数 可取值为0,1,2,3
可取值为0,1,2,3

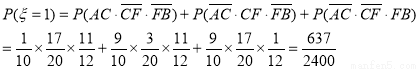
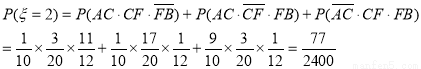

所以
故路线A→C→F→B中遇到堵车次数的数学期望为
考点:1、对立时间的概率;2、离散型随机变量的分布列、期望.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年上海市普陀区高三上学期质量调研理科数学试卷(解析版) 题型:填空题
设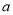 为大于
为大于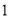 的常数,函数
的常数,函数 ,若关于
,若关于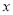 的方程
的方程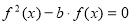 恰有三个不同的实数解,则实数
恰有三个不同的实数解,则实数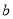 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市高三1月模拟理科数学试卷(解析版) 题型:填空题
由 ,
,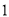 ,
,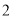 ,…,
,…,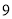 这十个数字组成的无重复数字的四位数中,十位数字与千位数字之差的绝对值等于
这十个数字组成的无重复数字的四位数中,十位数字与千位数字之差的绝对值等于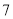 的四位数的个数是 .
的四位数的个数是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省广州市高三1月模拟理科数学试卷(解析版) 题型:选择题
将函数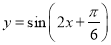 的图象向左平移
的图象向左平移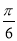 个单位,再向上平移
个单位,再向上平移 个单位,所得图象的函数解析式是( )
个单位,所得图象的函数解析式是( )
A.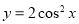 B.
B.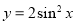
C.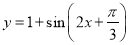 D.
D.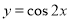
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西宝鸡卧龙寺中学高二上学期期末命题比赛数学试卷(解析版) 题型:解答题
(本题满分12分)某出版社的11名工人中,有5人只会排版,4人只会印刷,还有2人既会排版又会印刷,现从11人中选4人排版,4人印刷,有多少种不同的选法?
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西宝鸡卧龙寺中学高二上学期期末命题比赛数学试卷(解析版) 题型:选择题
对于线性相关系数r,不列说法正确的是( )
A.|r|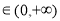 ,|r|越大,相关程度越大;反之相关程度越小
,|r|越大,相关程度越大;反之相关程度越小
B.|r| ,|r|越大,相关程度越大;反之相关程度越小
,|r|越大,相关程度越大;反之相关程度越小
C.|r| ,且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小
,且|r|越接近于1,相关程度越大;|r|越接近于0,相关程度越小
D.以上说法都不正确
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东枣庄薛城舜耕中学高一上学期10月月考数学试卷(解析版) 题型:填空题
已知函数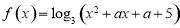 ,
,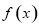 在区间
在区间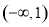 上是递减函数,则实数
上是递减函数,则实数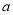 的取值范围为_________.
的取值范围为_________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省高二10月月考数学试卷(解析版) 题型:填空题
关于数列有下列命题:
(1)数列{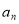 }的前n项和为
}的前n项和为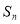 ,且
,且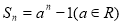 ,则{
,则{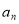 }为等差或等比数列;
}为等差或等比数列;
(2)数列{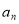 }为等差数列,且公差不为零,则数列{
}为等差数列,且公差不为零,则数列{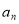 }中不会有
}中不会有 ,
,
(3)一个等差数列{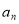 }中,若存在
}中,若存在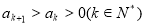 ,则对于任意自然数
,则对于任意自然数 ,都有
,都有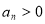 ;
;
(4)一个等比数列{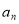 }中,若存在自然数
}中,若存在自然数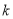 ,使
,使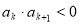 ,则对于任意
,则对于任意 ,都有
,都有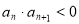 ,
,
其中正确命题的序号是___ __。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com