
分析 (Ⅰ)由两端不站女生,得到两端的位置共有$A_5^2$种排法,余下的6个位置共有$A_6^6$种不同的排法,由此利用分步计数原理,能求出女生不站在两端的不同的站法总数.
(Ⅱ)①记“选定的4人中至少有1名女生“为事件A,利用对立事件概率计算公式能求出选定的4人中至少有1名女生的概率.
②记“选定的4人中恰有2名男生且这2名男生来自同一所中学“为事件B,利用互斥事件概率加法公式能求出选定的4人中恰有2名男生且这2名男生来自同一所中学的概率.
解答 解:(Ⅰ)∵两端不站女生,∴两端的位置共有$A_5^2$种排法,
余下的6个位置共有$A_6^6$种不同的排法,
再根据分步计数原理,共有$A_5^2A_6^6=14400$种不同的排法. …(4分)
(Ⅱ)①记“选定的4人中至少有1名女生“为事件A,
则$P(A)=1-\frac{C_5^4}{C_8^4}=\frac{13}{14}$,
∴选定的4人中至少有1名女生的概率为$\frac{13}{14}$.…(8分)
②记“选定的4人中恰有2名男生且这2名男生来自同一所中学“为事件B,
则$P(B)=\frac{C_2^2C_3^2+C_3^2C_3^2}{C_8^4}=\frac{12}{70}=\frac{6}{35}$,
∴选定的4人中恰有2名男生且这2名男生来自同一所中学的概率为$\frac{6}{35}$.…(12分)
点评 本题考查分步计数原理的应用,考查概率的求法,是中档题,解题时要认真审题,注意对立事件概率计算公式和互斥事件概率加法公式的合理运用.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 81 | B. | 171 | C. | 231 | D. | 371 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知两灯塔A,D相距20海里,甲、乙两船同时从灯塔A处出发,分别沿与AD所成角相等的两条航线AB,AC航行,经过一段时间分别到达B,C两处,此时恰好B,D,C三点共线,且∠ABD=$\frac{π}{3}$,∠ADC=$\frac{7π}{12}$,则乙船航行的距离AC为( )
如图,已知两灯塔A,D相距20海里,甲、乙两船同时从灯塔A处出发,分别沿与AD所成角相等的两条航线AB,AC航行,经过一段时间分别到达B,C两处,此时恰好B,D,C三点共线,且∠ABD=$\frac{π}{3}$,∠ADC=$\frac{7π}{12}$,则乙船航行的距离AC为( )| A. | 10$\sqrt{6}$+10$\sqrt{2}$海里 | B. | 10$\sqrt{6}$-10$\sqrt{2}$海里 | C. | 40海里 | D. | 10$\sqrt{6}$+10$\sqrt{3}$海里 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
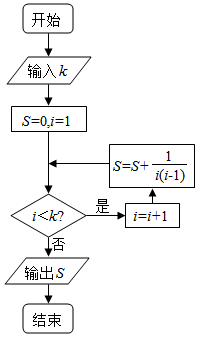
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
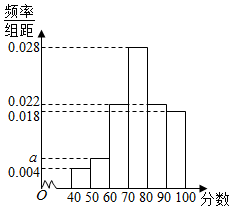 如图是根据某班50名同学在某次数学测验中的成绩(百分制)绘制的概率分布直方图,其中成绩分组区间为:[40,50),[50,60),…,[80,90),[90,100].
如图是根据某班50名同学在某次数学测验中的成绩(百分制)绘制的概率分布直方图,其中成绩分组区间为:[40,50),[50,60),…,[80,90),[90,100].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com