
分析 (Ⅰ)设Q(t,-2),A(x1,y1),B(x2,y2),由y′=$\frac{1}{2}$x,利用导数的几何意义求出在点A处的切线方程为y=$\frac{1}{2}$x1x-y1.在点B处的切线方程为y=$\frac{1}{2}$x2x-y2.从而点A,B都满足方程-2=$\frac{1}{2}$tx-y,由此能证明直线AB恒过定点(0,2).
(Ⅱ)设Q(x,y),则x1+x2=2x,y1+y2=2y,把A(x1,y1),B(x2,y2)代入x2=4y,利用点差法能求出Q点轨迹方程.
解答 证明:(Ⅰ)设Q(t,-2),A(x1,y1),B(x2,y2).
∵y=$\frac{1}{4}$x2,∴y′=$\frac{1}{2}$x.
∴在点A处的切线方程为y-y1=$\frac{1}{2}$x1(x-x1),化为y=$\frac{1}{2}$x1x-y1.
同理在点B处的切线方程为y=$\frac{1}{2}$x2x-y2.
∵点Q(t,-2)在两条切线上.
∴点A,B都满足方程-2=$\frac{1}{2}$tx-y,
∴直线AB恒过定点(0,2).
解:(Ⅱ)设Q(x,y),则x1+x2=2x,y1+y2=2y,
把A(x1,y1),B(x2,y2)代入x2=4y,
得$\left\{\begin{array}{l}{{{x}_{1}}^{2}=4{y}_{1}}\\{{{x}_{2}}^{2}=4{y}_{2}}\end{array}\right.$,两式相减,得(x1-x2)(x1+x2)=4(y1-y2),
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{2x}{4}$=$\frac{1}{2}x$,
∵直线AB过Q(x,y),(0,2),∴k=$\frac{y-2}{x}$,
∴$\frac{1}{2}x=\frac{y-2}{x}$,整理,得:x2-2y+4=0,
当直线AB的斜率不存在时,上式也成立,
∴Q点轨迹方程为x2-2y+4=0.
点评 本题考查直线恒过定点的证明,考查点的轨迹方程的求法,考查抛物线、导数的几何意义、点差法等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
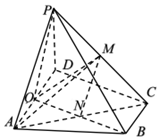 如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,BQ∩AC=N,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.
如图在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,BQ∩AC=N,M是棱PC上的一点,PA=PD=4=AD=2BC,CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
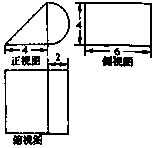
| A. | 24+6πcm3 | B. | 24+12πcm3 | C. | 48+12πcm3 | D. | 96+12πcm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {-2,-1,0,1} | C. | {0,1,2,3} | D. | {0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com