
分析 设C(2,y1),D(-2,y2),求出直线CD的方程,根据切线的性质得出y1y2=4,设M(x0,y0),用M点坐标表示出y1,y2,代入y1y2=4得出轨迹方程.
解答 解:设C(2,y1),D(-2,y2),则直线CD的方程为y-y1=$\frac{{y}_{1}-{y}_{2}}{4}$(x-2),
即(y1-y2)x-4y+2(y1+y2)=0,
∵直线CD与圆x2+y2=4相切,
∴$\frac{2|{y}_{1}+{y}_{2}|}{\sqrt{({y}_{1}-{y}_{2})^{2}+16}}$=2,整理得y1y2=4.
设M(x0,y0),则直线AM的方程为y=$\frac{{y}_{0}}{{y}_{0}+2}$(x+2),
令x=2得y=$\frac{4{y}_{0}}{{x}_{0}+2}$,即y1=$\frac{4{y}_{0}}{{x}_{0}+2}$,
同理得y2=$\frac{-4{y}_{0}}{{x}_{0}-2}$,
∵y1y2=4.
∴$\frac{4{y}_{0}}{{x}_{0}+2}$•$\frac{-4{y}_{0}}{{x}_{0}-2}$=4,
即x02+4y02=4,即$\frac{{{x}_{0}}^{2}}{4}$+y02=1.
∴M的轨迹方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1(x≠±2).
故答案为:$\frac{{x}^{2}}{4}+{y}^{2}$=1(x≠±2).
点评 本题考查了轨迹方程的求解,直线与圆的位置关系,属于中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:解答题
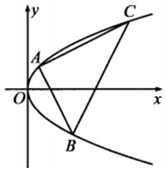 已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.
已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 72 | B. | 144 | C. | 150 | D. | 300 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 认为作业多 | 认为作业不多 | 总计 | |
| 喜欢玩游戏 | 20 | 10 | |
| 不喜欢玩游戏 | 2 | 8 | |
| 总计 |
| P(x2≥k) | 0.100 0.050 0.010 |
| k | 2.706 3.841 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ | D. | $-\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com