
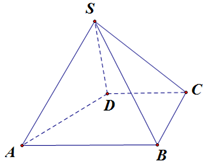
 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.分析 (Ⅰ) 取AB的中点E,连结DE,SE,则四边形BCDE为矩形,推导出SD⊥SA,SD⊥SB,由此能证明SD⊥平面SAB.
(Ⅱ)设四棱锥S-ABCD的高为h,则h也是三棱锥S-ABD的高,由VS-ABD=VD-SAB,能求了四棱锥S-ABCD的高.
解答 证明:(Ⅰ) 如图,取AB的中点E,连结DE,SE,则四边形BCDE为矩形,
∴DE=CB=2,∴$AD=\sqrt{D{E^2}+A{E^2}}=\sqrt{5}$,
∵侧面SAB为等边三角形,AB=2,
∴SA=SB=AB=2,且$SE=\sqrt{3}$,
又∵SD=1,∴SA2+SD2=AD2,SB2+SD2=BD2,
∴SD⊥SA,SD⊥SB,
∵SA∩SB=S,∴SD⊥平面SAB.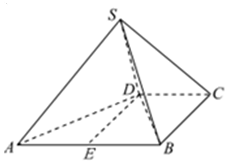
解:(Ⅱ)设四棱锥S-ABCD的高为h,则h也是三棱锥S-ABD的高,
由(Ⅰ)知,SD⊥平面SAB,
由VS-ABD=VD-SAB,得$\frac{1}{3}{S_{△ABD}}•h=\frac{1}{3}{S_{△SAB}}•SD$,
∴$h=\frac{{{S_{△SAB}}•SD}}{{{S_{△ABD}}}}$,
又${S_{△ABD}}=\frac{1}{2}AB•DE=\frac{1}{2}×2×2=2$,${S_{△SAB}}=\frac{{\sqrt{3}}}{4}A{B^2}=\frac{{\sqrt{3}}}{4}×{2^2}=\sqrt{3}$,SD=1,
∴$h=\frac{{{S_{△SAB}}•SD}}{{{S_{△ABD}}}}=\frac{{\sqrt{3}×1}}{2}=\frac{{\sqrt{3}}}{2}$,
故四棱锥S-ABCD的高为$\frac{{\sqrt{3}}}{2}$.
点评 本题考查线面垂直的证明,考查四棱锥的高的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $81-27\sqrt{3}$ | B. | 54 | C. | 38-1 | D. | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,+∞) | B. | (-2,+∞) | C. | (-∞,-4) | D. | (-∞,-4] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 15 | 16 | 18 | 19 | 22 |
| y | 102 | 98 | 115 | 115 | 120 |
| A. | 点在直线左侧 | B. | .点在直线右侧 | C. | .点在直线上 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com