
分析 (Ⅰ)由直线l经过点P(-1,0),且倾斜角为α,可得直线l的参数方程,利用互化公式可得C的直角坐标方程.由直线l与曲线C有公共点,可得△=64cos2α-32≥0,解出即可得出的取值范围;
(Ⅱ)设M(x,y)为曲线C上任意一点,利用参数方程为$\left\{{\begin{array}{l}{x=3+2\sqrt{2}cosθ}\\{y=2\sqrt{2}sinθ}\end{array}}\right.$(θ为参数),结合三角函数知识求x+y的取值范围.
解答 解:(Ⅰ)∵曲线C的极坐标方程为ρ2-6ρcosθ+1=0,∴曲线C的直角坐标方程为x2+y2-6x+1=0
∵直线l经过点P(-1,0),其倾斜角为α,∴直线l的参数方程为$\left\{{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}}\right.$(t为参数)
将$\left\{{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}}\right.$,代入x2+y2-6x+1=0整理得t2-8tcosα+8=0
∵直线l与曲线C有公共点,∴△=64cos2α-32≥0即$cosα≥\frac{{\sqrt{2}}}{2}$或$cosα≤-\frac{{\sqrt{2}}}{2}$
∵α∈[0,π)∴α的取值范围是$[{0,\frac{π}{4}}]∪[{\frac{3π}{4},π})$…(5分)
(Ⅱ)曲线C的直角坐标方程为x2+y2-6x+1=0可化为(x-3)2+y2=8
其参数方程为$\left\{{\begin{array}{l}{x=3+2\sqrt{2}cosθ}\\{y=2\sqrt{2}sinθ}\end{array}}\right.$(θ为参数) …(7分)
∵M(x,y)为曲线C上任意一点,∴$x+y=3+2\sqrt{2}cosθ+2\sqrt{2}sinθ=3+4sin(θ+\frac{π}{4})$
∴x+y的取值范围是[-1,7].…(10分)
点评 本题考查了极坐标化为直角坐标方程、参数方程的运用,考查了推理能力与计算能力,属于中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{{π^2}+4}$ | B. | π | C. | 2 | D. | $\sqrt{{π^2}+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
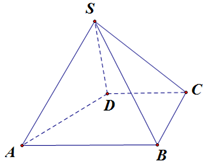 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=SD=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com