
【题目】已知圆![]() ,圆N与圆M关于直线
,圆N与圆M关于直线![]() 对称.
对称.
(1)求圆N的方程.
(2)是否存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,使得
,使得![]() 被圆M截得的弦长与
被圆M截得的弦长与![]() 被圆N截得的弦长相等?若存在,求出点P的坐标;若不存在,请说明理由.
被圆N截得的弦长相等?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)存在,
(2)存在,![]() 或
或![]()
【解析】
(1)求出圆心![]() 的对称点
的对称点![]() 即可得;
即可得;
(2)假设存在,设![]() ,分析直线的性质,题意说明圆心到相交直线的距离相等,即
,分析直线的性质,题意说明圆心到相交直线的距离相等,即![]() 到
到![]() 的距离等于
的距离等于![]() 到直线
到直线![]() 的距离,为此设直线
的距离,为此设直线![]() 的方程为
的方程为![]() ,
,![]() (考虑斜率存在且不为0),由点到直线距离公式得一关于斜率
(考虑斜率存在且不为0),由点到直线距离公式得一关于斜率![]() 的恒等式,可求得
的恒等式,可求得![]() .
.
(1)设![]() ,
,![]() 圆M与圆N关于直线
圆M与圆N关于直线![]() 对称,
对称,![]() ,
,
则直线MN与直线l垂直,MN的中点在直线l上,得 ,
,
解得![]() ,
,![]() 圆
圆![]() .
.
(2)设点![]() 满足条件,
满足条件,
假设直线![]() ,
,![]() 的斜率均存在且不为0,
的斜率均存在且不为0,
不妨设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
则直线![]() 的方程为
的方程为![]() .
.
![]() 圆M和圆N的半径相等,且直线
圆M和圆N的半径相等,且直线![]() 被圆M截得的弦长与直线
被圆M截得的弦长与直线![]() 被圆N截得的弦长相等,
被圆N截得的弦长相等,
![]() 圆M的圆心到直线
圆M的圆心到直线![]() 的距离和圆N的圆心到直线
的距离和圆N的圆心到直线![]() 的距离相等,
的距离相等,
即 ,
,
整理得![]() ,
,
![]() ,即
,即![]() 或
或![]() ,
,
![]() 的取值有无穷多个,
的取值有无穷多个,![]() 或
或![]() ,
,
解得![]() 或
或![]() .
.
这样的点只可能是点![]() 或点
或点![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 和
和![]() 同时在
同时在![]() 处取得极小值,则称
处取得极小值,则称![]() 和
和![]() 为一对“
为一对“![]() 函数”.
函数”.
(1)试判断![]() 与
与![]() 是否是一对“
是否是一对“![]() 函数”;
函数”;
(2)若![]() 与
与![]() 是一对“
是一对“![]() 函数”.
函数”.
①求![]() 和
和![]() 的值;
的值;
②当![]() 时,若对于任意
时,若对于任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
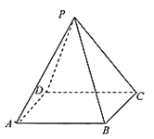
【题目】已知正四棱锥![]() 的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量
的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量![]() 表示所得三角形的面积.
表示所得三角形的面积.
(1)求概率![]() 的值;
的值;
(2)求随机变量![]() 的概率分布及其数学期望
的概率分布及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为 .
.
(1)求![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() 两点(
两点(![]() 在第一象限),以
在第一象限),以![]() 为直径的圆分别与
为直径的圆分别与![]() 轴相切于
轴相切于![]() 两点,则下列结论正确的是( )
两点,则下列结论正确的是( )
A.抛物线![]() 的焦点
的焦点![]() 坐标为
坐标为![]() B.
B.![]()
C.![]() 为抛物线
为抛物线![]() 上的动点,
上的动点,![]() ,则
,则![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
, .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,
,![]() ,若
,若![]() ,
,![]() ,则称
,则称![]() 是
是![]() 的“收缩数列”.其中
的“收缩数列”.其中![]() ,
,![]() 分别表示
分别表示![]() 中的最大数和最小数.已知
中的最大数和最小数.已知![]() 为无穷数列,其前
为无穷数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是
是![]() 的“收缩数列”.
的“收缩数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() ;
;
(3)若![]() 且
且![]() ,
,![]() ,求所有满足该条件的
,求所有满足该条件的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com