
分析 (1)利用柯西不等式直接证明即可.
(2)法一:利用分析法,不妨设a≥b≥c≥d,直接证明即可.
法二:利用$\frac{a^2}{b}+b≥2a$,$\frac{b^2}{c}+c≥2b$,$\frac{c^2}{d}+d≥2c$,$\frac{d^2}{a}+a≥2d$,然后求和证明即可.
解答 证明:(1)∵(a2+b2+c2+d2)•(1+1+1+1)≥(a+b+c+d)2=1,
∴${a^2}+{b^2}+{c^2}+{d^2}≥\frac{1}{4}$当且仅当$a=b=c=d=\frac{1}{4}$时,等号成立…(6分)
(2)(法一)不妨设a≥b≥c≥d,则a2≥b2≥c2≥d2,$\frac{1}{d}≥\frac{1}{c}≥\frac{1}{b}≥\frac{1}{a}$,
$\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{d}+\frac{d^2}{a}≥\frac{a^2}{a}+\frac{b^2}{b}+\frac{c^2}{c}+\frac{d^2}{d}=a+b+c+d=1$,
当且仅当$a=b=c=d=\frac{1}{4}$时,等号成立…(12分)
(法二)∵$\frac{a^2}{b}+b≥2a$,$\frac{b^2}{c}+c≥2b$,$\frac{c^2}{d}+d≥2c$,$\frac{d^2}{a}+a≥2d$,
以上各式相加得,$\frac{a^2}{b}+b+\frac{b^2}{c}+c+\frac{c^2}{d}+d+\frac{d^2}{a}+a≥2a+2b+2c+2d$,
即$\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{d}+\frac{d^2}{a}≥a+b+c+d$,
当且仅当$a=b=c=d=\frac{1}{4}$时,等号成立…(12分)
点评 本题考查不等式的证明,柯西不等式以及分析法与综合法的应用,考查逻辑推理能力.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | (-∞,2] | C. | 10,+∞) | D. | 12,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
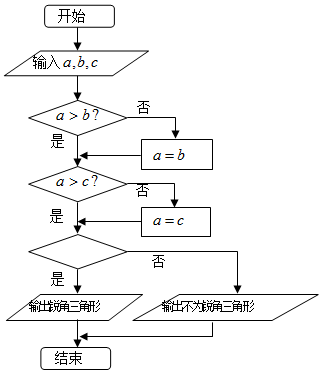 下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )
下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )| A. | a2+b2>c2? | B. | a2+c2>b2? | C. | b2+c2>a2? | D. | b2+a2=c2? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | af(b)>bf(a) | B. | bf(a)>af(b) | C. | af(a)<bf(b) | D. | af(a)>bf(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )| A. | 丙在Ⅲ区域,丁在Ⅰ区域 | B. | 丙在Ⅰ区城,丁在Ⅲ区域 | ||
| C. | 丙在Ⅱ区域,丁在Ⅰ区域 | D. | 丙在Ⅲ区域,丁在Ⅱ区域 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com