
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
分析 由f(x)=1+$\frac{{e}^{x}sinx}{1+{e}^{2x}}$,令g(x)=$\frac{{e}^{x}sinx}{1+{e}^{2x}}$,x∈R,判断g(x)为奇函数,其最值之和为0,即可得到所求和.
解答 解:函数$f(x)=\frac{{{e^{2x}}-{e^x}sinx+1}}{{{e^{2x}}+1}}$
=1+$\frac{{e}^{x}sinx}{1+{e}^{2x}}$,
令g(x)=$\frac{{e}^{x}sinx}{1+{e}^{2x}}$,x∈R,
则g(-x)=$\frac{{e}^{-x}sin(-x)}{1+{e}^{-2x}}$=$\frac{{e}^{x}(-sinx)}{{e}^{2x}+1}$=-g(x),
可得g(x)为奇函数,
由奇函数的图象关于原点对称,可得g(x)的最大值A和最小值a之和为0,
则M+m=(A+1)+(a+1)=(A+a)+2=2.
故选:C.
点评 本题考查函数的最值的求法,注意运用转化思想和构造函数法,运用奇函数的图象关于原点对称,其最值之和为0是解题的关键,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
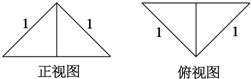 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的正视图与俯视图如图所示,则其侧视图的面积为$\frac{1}{4}$,二面角B-AC-D的余弦值为$-\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab>b2 | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | $\frac{1}{a}$<$\frac{1}{b}$ | D. | a2>ab |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 5 | 10 | 15 | 47 | x |
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000) |
| 人数 | 2 | 3 | 10 | y | 2 |
| 女性 | 男性 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com