
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左顶点、右焦点,点
的左顶点、右焦点,点![]() 为椭圆
为椭圆![]() 上一动点,当
上一动点,当![]() 轴时,
轴时, ![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若椭圆![]() 存在点
存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形(点
是平行四边形(点![]() 在第一象限),求直线
在第一象限),求直线![]() 与
与![]() 的斜率之积;
的斜率之积;
(3)记圆![]() 为椭圆
为椭圆![]() 的“关联圆”. 若
的“关联圆”. 若![]() ,过点
,过点![]() 作椭圆
作椭圆![]() 的“关联圆”的两条切线,切点为
的“关联圆”的两条切线,切点为![]() 、
、![]() ,直线
,直线![]() 的横、纵截距分别为
的横、纵截距分别为![]() 、
、![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:
(1)利用题意得到关于![]() 的齐次方程,求解方程组可得椭圆的离心率
的齐次方程,求解方程组可得椭圆的离心率![]() ;
;
(2) 由题意, ![]() ,
, ![]() ,则
,则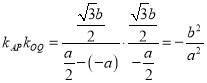 ,结合(1)的结论可得
,结合(1)的结论可得![]() .
.
(3) 由(1)知椭圆![]() 方程为
方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() .
.
四边形![]() 的外接圆方程为
的外接圆方程为![]() ,
,
所以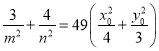 ,因为点
,因为点![]() 在椭圆
在椭圆![]() 上,则
上,则![]() .
.
试题解析:
解:(1)由![]() 轴,知
轴,知![]() ,代入椭圆
,代入椭圆![]() 的方程,
的方程,
得![]() ,解得
,解得![]() .
.
又![]() ,所以
,所以![]() ,解得
,解得![]() .
.
(2)因为四边形![]() 是平行四边形,所以
是平行四边形,所以![]() 且
且![]() 轴,
轴,
所以![]() ,代入椭圆
,代入椭圆![]() 的方程,解得
的方程,解得![]() , 因为点
, 因为点![]() 在第一象限,所以
在第一象限,所以![]() ,同理可得
,同理可得![]() ,
, ![]() , 所以
, 所以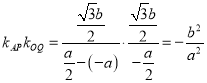 ,
,
由(1)知![]() ,得
,得![]() ,所以
,所以![]() .
.
(3)由(1)知![]() ,又
,又![]() ,解得
,解得![]() ,所以椭圆
,所以椭圆![]() 方程为
方程为![]() ,
,
圆![]() 的方程为
的方程为![]() ①. 连接
①. 连接![]() ,由题意可知,
,由题意可知, ![]() ,
, ![]() ,
,
所以四边形![]() 的外接圆是以
的外接圆是以![]() 为直径的圆,
为直径的圆,
设![]() ,则四边形
,则四边形![]() 的外接圆方程为
的外接圆方程为![]() ,
,
即![]() ②. ①-②,得直线
②. ①-②,得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() . 所以
. 所以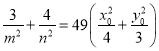 ,
,
因为点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2( ![]() +x)+
+x)+ ![]() (sin2x﹣cos2x),x∈[
(sin2x﹣cos2x),x∈[ ![]() ,
, ![]() ].
].
(1)求 ![]() 的值;
的值;
(2)求f(x)的单调区间;
(3)若不等式|f(x)﹣m|<2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
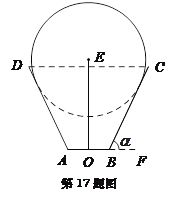
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的右顶点为
的右顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,过点
,过点![]()
且斜率为![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() , 与椭圆交于另一个点
, 与椭圆交于另一个点![]() ,且点
,且点![]() 在
在![]() 轴上的射影恰好为点
轴上的射影恰好为点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 且斜率大于
且斜率大于![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点(
两点(![]() ),若
),若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研机构研发了某种高新科技产品,现已进入实验阶段.已知实验的启动资金为10万元,从实验的第一天起连续实验,第![]() 天的实验需投入实验费用为
天的实验需投入实验费用为![]() 元
元![]() ,实验30天共投入实验费用17700元.
,实验30天共投入实验费用17700元.
(1)求![]() 的值及平均每天耗资最少时实验的天数;
的值及平均每天耗资最少时实验的天数;
(2)现有某知名企业对该项实验进行赞助,实验![]() 天共赞助
天共赞助![]() 元
元![]() .为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求
.为了保证产品质量,至少需进行50天实验,若要求在平均每天实际耗资最小时结束实验,求![]() 的取值范围.(实际耗资=启动资金+试验费用-赞助费)
的取值范围.(实际耗资=启动资金+试验费用-赞助费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com