
【题目】在直角坐标系xOy中,以原点O为极点,以x轴正半轴为极轴,曲线C的极坐标方程为ρ= ![]() . (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
. (Ⅰ)将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)过点P(0,2)作斜率为1直线l与曲线C交于A,B两点,试求 ![]() +
+ ![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】自然数按如图的规律排列:则上起第2007行左起2008列的数为( ) 
A.20072
B.20082
C.2006×2007
D.2007×2008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6 , 及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和直线
和直线![]() :
: ![]() ,椭圆的离心率
,椭圆的离心率![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() .
.

(Ⅰ)求椭圆的方程;
(Ⅱ)已知定点![]() ,若直线
,若直线![]() 过点
过点![]() 且与椭圆相交于
且与椭圆相交于![]() 两点,试判断是否存在直线
两点,试判断是否存在直线![]() ,使以
,使以![]() 为直径的圆过点
为直径的圆过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为(0,+∞)的函数f(x)满足:(1)对任意x∈(0,+∞),恒有f(2x)=2f(x)成立;(2)当x∈(1,2]时,f(x)=2﹣x. 给出如下结论:
①对任意m∈Z,有f(2m)=0;
②函数f(x)的值域为[0,+∞);
③存在n∈Z,使得f(2n+1)=9;
正确的有( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱。现统计了连续5天的售出和收益情况,如下表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(Ⅰ) 若x与y成线性相关,则某天售出8箱水时,预计收益为多少元?
(Ⅱ) 期中考试以后,学校决定将诚信用水的收益,以奖学金的形式奖励给品学兼优的特困生,规定:特困生考入年级前200名,获一等奖学金500元;考入年级201—500 名,获二等奖学金300元;考入年级501名以后的特困生将不获得奖学金。甲、乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() .
.
⑴在学生甲获得奖学金条件下,求他获得一等奖学金的概率;
⑵已知甲、乙两名学生获得哪个等第的奖学金是相互独立的,求甲、乙两名学生所获得奖学金总金额X 的分布列及数学期望。
附: 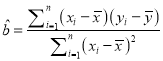 ,
, ![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学为了解本校某年级女生的身高情况,从本校该年级的学生中随机选出100名女生并统计她们的身高(单位: ![]() ),得到下面的频数分布表:
),得到下面的频数分布表:

(1)用分层抽样的方法从身高在![]() 和
和![]() 的女生中共抽取6人,则身高在
的女生中共抽取6人,则身高在![]() 的女生应抽取几人?
的女生应抽取几人?
(2)在(1)中抽取的6人中,再随机抽取2人,求这2人身高都在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(﹣4,0),D(0,4)设△AOB的外接圆圆心为E. 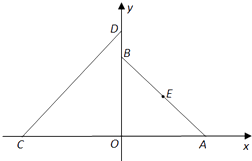
(1)若⊙E与直线CD相切,求实数a的值;
(2)设点P在圆E上,使△PCD的面积等于12的点P有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 底面
底面![]() ,
, ![]() ,且
,且![]() .
.
(Ⅰ)记线段![]() 的中点为
的中点为![]() ,在平面
,在平面![]() 内过点
内过点![]() 作一条直线与平面
作一条直线与平面![]() 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com