
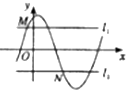
 如图,M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m(A≥m≥0),l2:y=-m的两个交点,记S(m)=|xM-xN|,则S(m)的图象大致是( )
如图,M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m(A≥m≥0),l2:y=-m的两个交点,记S(m)=|xM-xN|,则S(m)的图象大致是( )| A. | 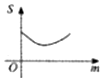 | B. | 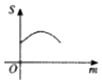 | C. | 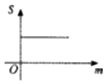 | D. |  |
分析 由已知条件及所给函数的图象知,图象从M点到N点的变化正好是半个周期,
故|xM-xN|=$\frac{T}{2}$,S(m)的图象大致是常函数.
解答 解:如图所示,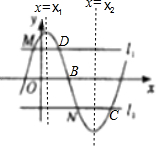
作曲线y=f(x)的对称轴x=x1,x=x2,
点M与点D关于直线x=x1对称,
点N与点C关于直线x=x2对称,
∴xM+xD=2x1,xC+xN=2x2;
∴xD=2x1-xM,xC=2x2-xN;
又点M与点C、点D与点N都关于点B对称,
∴xM+xC=2xB,xD+xN=2xB,
∴xM+2x2-xN=2xB,
2x1-xM+xN=2xB,
∴xM-xN=2(xB-x2)=-$\frac{T}{2}$,
∴xN-xM=2(xB-x1)=$\frac{T}{2}$,
∴|xM-xN|=$\frac{T}{2}$,T为f(x)的最小正周期;
S(m)的图象大致是常数函数.
故选:C.
点评 本题主要考查了三角函数的图象与性质的应用问题,也考查了转化思想与数形结合的应用问题,是综合性题目.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:填空题
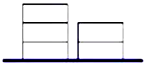 如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).
如图,在地上有同样大小的5块积木,一堆2个,一堆3个,要把积木一块一块的全部放到某个盒子里,每次只能取出其中一堆最上面的一块,则不同的取法有10种(用数字作答).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,3] | B. | [-2,0] | C. | [1,3] | D. | [0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
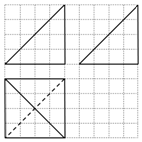
| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,3] | B. | (-1,3] | C. | (0,1] | D. | (0,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com