练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．执行如图所示的程序框图，输出S的值为（　　）
    A．log210-1B．2log23-1C．$\frac{9}{2}$D．6

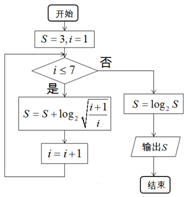
    分析 由题意，模拟程序的运行过程，依次写出每次循环得到的S，i的值，即可得出跳出循环时输出S的值．

    解答 解：模拟程序的运行，可得：
    由$lo{g_2}\sqrt{\frac{i+1}{i}}=\frac{1}{2}[lo{g_2}（i+1）-lo{g_2}i]$，
    当i=7时，进入循环，得$S=3+\frac{1}{2}[lo{g_2}\frac{2}{1}+$$lo{g_2}\frac{3}{2}+…+lo{g_2}\frac{8}{7}]=3+\frac{1}{2}[（lo{g_2}2-lo{g_2}1）+（lo{g_2}3-lo{g_2}2）+…+（lo{g_2}8-lo{g_2}7）]=\frac{9}{2}$，
    当i=8退出循环，输出$S=lo{g_2}\frac{9}{2}=2lo{g_2}3-1$，
    故选：B．

    点评 本题主要考查了循环结构的程序框图应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=2cosx（sinx+cosx），x∈R．
    （Ⅰ）求函数f（x）的最小正周期；
    （Ⅱ）求函数f（x）的单调递增区间；
    （Ⅲ）求函数f（x）在区间[-$\frac{π}{4}$，$\frac{π}{4}$]上的最小值和最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

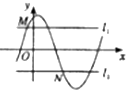    11．如图，M（xM，yM），N（xN，yN）分别是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与两条直线l1：y=m（A≥m≥0），l2：y=-m的两个交点，记S（m）=|xM-xN|，则S（m）的图象大致是（　　）
    A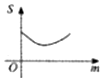．B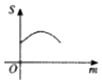．C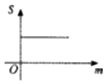．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知实数x，y满足$\left\{\begin{array}{l}3x-2y-3≤0\\ x-3y+6≥0\\ 2x+y-2≥0\end{array}\right.$，在这两个实数x，y之间插入三个实数，使这五个数构成等差数列，那么这个等差数列后三项和的最大值为9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知数列{an}，a1=1，${a_{n+1}}=\frac{{2{a_n}}}{{{a_n}+2}}$，则a10的值为（　　）
    A．5B．$\frac{1}{5}$C．$\frac{11}{2}$D．$\frac{2}{11}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知等差数列{an}的前n项和为Sn，且a1=1，S3+S4=S5．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）令bn=（-1）n-1anan+1，求数列{bn}的前2n项和T2n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知抛物线y2=2px（p＞0），焦点到准线的距离为4，过点P（1，-1）的直线交抛物线于A，B两点．
    （Ⅰ）求抛物线的方程；
    （Ⅱ）如果点P恰是线段AB的中点，求直线AB的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知函数f（x）=logax（0＜a＜1），则函数y=f（|x|+1）的图象大致为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．执行如图所示的程序框图，若输出的y值为-1，则输入的x值为（　　）
    A．$\frac{1}{2}$B．1C．$\sqrt{2}$D．2

    查看答案和解析>>

    同步练习册答案